Inför tentamen i Aritmetik & Algebra, del 2, VT 00.

Kursmaterialet betstår av kompendiet Aritmetik och algebra, kapitel 4.3-8.6 (utom 8.4), samt Vretblads bok Algebra och geometri (kapitel 8.1-3).

Samtliga satser och definitioner som ingår i kursmaterialet ska kunna formuleras. Följande satser ur kompendiet ska kunna formuleras och bevisas:

Sats 4.28 (Utgångspunkten för uppdelning i partialbråk), sid.90
Sats 6.3 (Faktorsatsen), sid. 124,
Sats 6.6 (Existens av faktorisering), sid. 128,
Sats 6.7 (Existens av SGD och Bezouts identitet), sid. 129,
Sats 6.9-10 (Faktoriseringens entydighet), sid. 131-132,
Sats 6.13 (Inverterbara element i K[x]/f), sid. 135,
Sats 6.17 (Olika rötter i 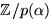$\mathbb Z/p(\alpha)$), sid. 139-140,
Sats 7.7 (Linjärt beroende lösningar), sid. 173-174,
Sats 7.15 (Egenvektorer till olika egenvärden är linjärt oberoende), sid. 185-186,
Sats 8.4 (Inverterbarhet av formell potensserie), sid. 201-202
Sats 8.8 (Lösning av en linjär rekursionsekvation), sid. 215-216.

Skrivningen kommer att bestå av åtta uppgifter om vardera tre poäng, utom en av uppgifterna som kan ge fyra poäng. Tre av uppgifterna är av teoretisk karaktär. Under kursen förekommer inlämningsuppgifter som kan ge högst två bonus poäng vid ordinarie tentamen (den 6 juni 2000). Bonuspoängen kan bara användas för att uppnå betyget godkänd. Maximala antalet poäng är alltså tjugofem. Gränsen för godkänd på del 2 är tolv och för väl godkänd arton.

För godkänt på hela kursen Aritmetik och algebra krävs godkänt resultat på de båda deltentorna. För välgodkänt krävs att den sammanlagda skrivningspoängen uppgår till minst trettiosex poäng.

Observera att vid tentamen är inga hjälpmedel tillåtna, inte ens räknedosa.