$\parbox{5cm}{Aritmetik och algebra\\ del 2, VT 98 \\ ~~~~\\ ~~~~}$

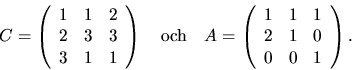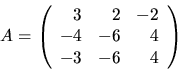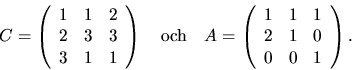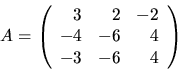
Inlämningsuppgift 2

1.

Bestäm en så liten kropp K som möjligt som innehåller 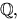$\mathbb Q,$så att polynomet $x^{4}-2x^{3}-3x^{2}+4x+2\in \mathbb Q[x]$faktoriserar som en produkt av polynom av grad 1 i K[x]. Ange faktoriseringen.

2.

Bestäm en så liten korpp K som möjligt som innehåller 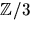$\mathbb Z/3$, så att polynomet $x^{3}+2x+1\in \mathbb Z/3[x]$ faktoriserar som en produkt av polynom av grad 1 i K[x]. Ange faktoriseringen.

3.

Matrisen C nedan är inveterbar. Lös ekvationen C^-1X=A, där

$$C=\left( \begin{array} {rrr}1&1&2\\ 2&3&3\\ 3&1&1\end{arr... ... \begin{array} {rrr}1&1&1\\ 2&1&0\\ 0&0&1\end{array}\right).$$

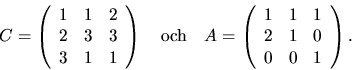
Matriserna har element i 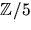$\mathbb Z/5$.

4.

Bestäm, om möjligt, en inverterbar matris C och en diagonal matris D, så att A=CDC^-1, när

$$A=\left( \begin{array} {rrr} 3&2&-2\\ -4&-6&4\\ -3&-6&4 \end{array}\right)$$

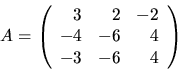
har element i 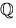$\mathbb Q$.

Lösningarna ska lämnas till respektive övningsledare senast den 18 maj.

Man kan få tre poäng per uppgift. Om totala antalet poäng på inlämingsuppgifterna är tolv eller mer får man ett bonuspoäng vid ordinarie tentamen. Har man arton eller mer får man två bonuspoäng.