- (a)
- Vi undersöker först om p(x)=x4+4x3+4x2+5x-2 har något
rationellt nollställe. Enligt Faktorsatsen motsvarar ett sådant en
faktor av grad 1. De möjliga rationella nollställena till p(x)
är
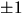 och
och 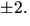 Vi ser genast att de negativa värdena är
uteslutna. Vi har också
Vi ser genast att de negativa värdena är
uteslutna. Vi har också 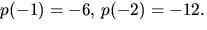 Därmed saknar
polynomet faktor av grad 1 (och följdaktligen faktor av grad
3.)
Därmed saknar
polynomet faktor av grad 1 (och följdaktligen faktor av grad
3.)
Vi undersöker om polynomet är produkt av två polynom av grad 2 genom att ansätta p(x)=(x2+ax+b)(x2+cx+d), där vi kan förutsätta att
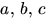 och d är heltal eftersom p(x) är
primitivt. Utveckling ger ekvationssystemet
och d är heltal eftersom p(x) är
primitivt. Utveckling ger ekvationssystemet
Den sista ekvationen ger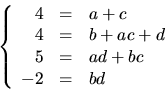
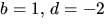 eller
eller 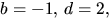 eller
motsvarande där b och d byter plats. Det första alternativet
ger 5=-2a+c i tredje ekvationen. Tillsammans med den första ger
detta -1=3a, som saknar heltaslösning. Alternativet
eller
motsvarande där b och d byter plats. Det första alternativet
ger 5=-2a+c i tredje ekvationen. Tillsammans med den första ger
detta -1=3a, som saknar heltaslösning. Alternativet 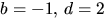 ger 5=2a-c i tredje ekvationen. Tillsammans med den första ger
detta
ger 5=2a-c i tredje ekvationen. Tillsammans med den första ger
detta 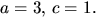 Vi ser att vi har en lösning till
ekvationssystemt och därmed faktoriseringen
Vi ser att vi har en lösning till
ekvationssystemt och därmed faktoriseringen
p(x)=(x2+3x-1)(x2+x+2)
där faktorerna är irreducibla eftersom p(x) saknar faktor av grad 1. - (b)
- Vi undersöker om p(x)=x4+3x3+2x2+x+3 har faktor av grad 1.
Enligt Faktorsatsen motsvarar en sådan ett rationellt
nollställe. De möjliga rationella nollställena är
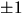 och
och 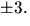 De positiva värdena är uteslutna. Vi har också p(-1)=2 och
p(-3)=18. Polynomet saknar alltså faktor av grad 1 (och
följdaktligen faktor av grad 3.)
De positiva värdena är uteslutna. Vi har också p(-1)=2 och
p(-3)=18. Polynomet saknar alltså faktor av grad 1 (och
följdaktligen faktor av grad 3.)
Vi undersöker om polynomet är produkt av två polynom av grad 2 genom att ansätta p(x)=(x2+ax+b)(x2+cx+d) där vi kan förutsätta att
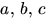 och d är heltal eftersom p(x) är
primitivt. Utvecklig ger ekvationssystemet
och d är heltal eftersom p(x) är
primitivt. Utvecklig ger ekvationssystemet
Den nedersta ekvationen ger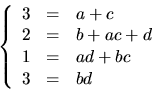
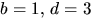 eller
eller 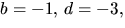 eller
motsvarande där b och d byter plats. Det första alternativiet
ger 1=3a+c i tredje ekvationen. Tillsammans med den första ger
detta
eller
motsvarande där b och d byter plats. Det första alternativiet
ger 1=3a+c i tredje ekvationen. Tillsammans med den första ger
detta 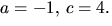 Men dessa värden strider mot den andra
ekvationen. Alternativet
Men dessa värden strider mot den andra
ekvationen. Alternativet 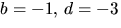 ger -1=3a+c i tredje
ekvationen. Tillsammans med den första ger detta
ger -1=3a+c i tredje
ekvationen. Tillsammans med den första ger detta 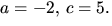 Dessa värden strider mot den andra ekvationen.
Dessa värden strider mot den andra ekvationen.
Vi har därmed visat att p(x) är irreducibelt.
- (c)
- Vi använder Eisensteins kriterium med primtalet 13. Detta tal
delar samtliga koefficienter i polynomet utom den ledande (som är
1.). Vi har nämligen
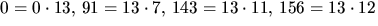 och
och 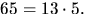 Vidare är det uppenbart
att 132 inte delar 65. Enligt Eisensteins kriterium är
polynomet därmed irreducibelt.
Vidare är det uppenbart
att 132 inte delar 65. Enligt Eisensteins kriterium är
polynomet därmed irreducibelt.
![]()
![]()
![]()
2i=A+Bi
dvs A=0 och B=2. Vi multiplicerar båda sidor med (x2-2)2 och sätter![]()
![]()
För att invertera bestämmer vi en största gemensam delare till polynomen
![]() och
och ![]() med Euklides
algoritm:
med Euklides
algoritm:
![]()
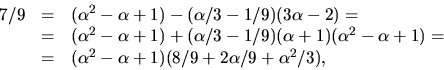
![]()
För att lösa ekvationen gör vi först en kvadratkomplettering och får
![]()
![]()
![]()
![]()
![]()