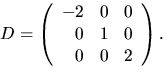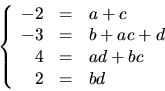
f(x)=x4-2x3-3x2+4x+2=(x2-2x-1)(x2-2)
som är en faktorisering med hjälp av irreducibla polynom.
Vi sätter ![]() där
där
![]() som är en kropp eftersom
som är en kropp eftersom ![]() är
irreducibelt. Polynomet f(x) har nollställena
är
irreducibelt. Polynomet f(x) har nollställena ![]() i K så
i K så
![]() Vi undersöker om x2-2x-1
har något nollställe i K. Kvardratkomplettering ger
0=x2-2x-1=(x-1)2-2 och vi ska lösa (x-1)2=2. Eftersom
Vi undersöker om x2-2x-1
har något nollställe i K. Kvardratkomplettering ger
0=x2-2x-1=(x-1)2-2 och vi ska lösa (x-1)2=2. Eftersom
![]() har vi
har vi ![]() dvs
dvs ![]() Vi får
Vi får
![]()
svar: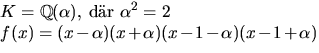
Vi beräkna ![]() och
och ![]()
![]()
![]()
svar: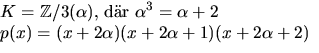
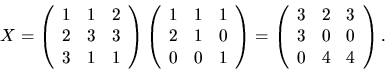
svar: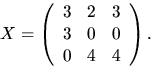
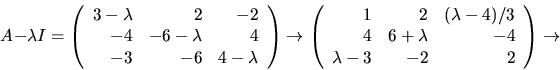
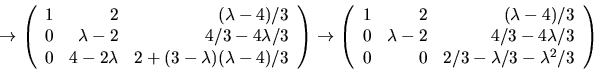
Vi bestämmer egenvärden till vart och ett av egenvärdena till A
genom att bestämma en lösning ![]() till
till
![]()
- (a)
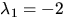 . Radoperationerna ovan ger
. Radoperationerna ovan ger
Vi ser att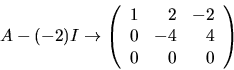
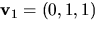 duger.
duger.
- (b)
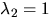 . Radoperationerna ovan ger
. Radoperationerna ovan ger
Vi ser att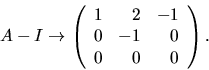
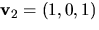 duger.
duger.
- (c)
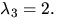 Radoperationerna ovan ger
Radoperationerna ovan ger
Vi ser att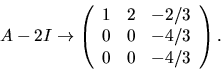
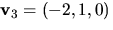 duger.
duger.
Vi har alltså att ![]() där D är
diagonal med
där D är
diagonal med ![]() och 2 längs huvuddiagonalen. Matrisen
och 2 längs huvuddiagonalen. Matrisen ![]() är inverterbar, ty
vektorerna hör till olika egenvärden.
är inverterbar, ty
vektorerna hör till olika egenvärden.
svar: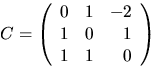 och
och