---

 

Ett exempel

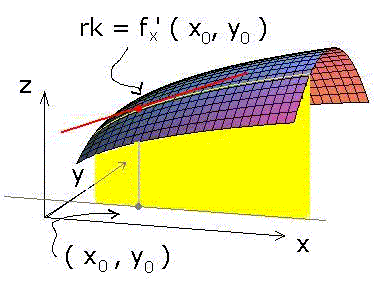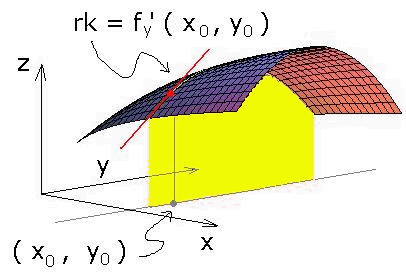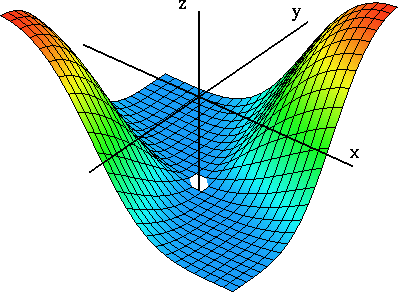
Figuren illustrerar grafen till funktionen   f( x, y) =  cos( x + y) - 1 + xy x 2 + y 2

En kalkyl visar att gränsvärdet av funktionen när  ( x, y)  ( 0, 0)  är  - 1 / 2  .   Om man sätter  f( 0, 0) =  1 / 2  blir funktionen kontinuerlig ( i origo).

---

 

Räkneregler för gränsvärden

Antag  k  är en reell konstant och att  f( x)b  och  g( x)c  när  xa . Då gäller att

1)  kf( x)kb   2)  f( x) + g( x)b + c   3)  f( x) g( x)bc   4)  f( x) / g( x)b / c  (om  c  0 )

när  xa .

---

 

Sats om kontinuitet

Antag att  k  är en reell konstant samt att  f( x)  och  g( x)  är kontinuerliga  a . Då gäller att

1)  kf( x)   2)  f( x) + g( x)   3)  f( x) g( x)   4)  f( x) / g( x)  (om  g( a)  0 )

samtliga är kontinuerliga i  a .

---

 

Partiell derivata map första koordinaten

Genom att fixera  y0  och låta  x  variera runt  x0  bestäms partialderivatan  fx' ( x0, y0 )  av  f  i punkten  ( x0, y0 ) .   Den ger ett mått på den relativa förändringen av  f  i  x -led i punkten  ( x0, y0 ) .

---

 

Partiell derivata map andra koordinaten

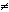Genom att fixera  x0  och låta  y  variera runt  y0  bestäms partialderivatan  fy' ( x0, y0 )  av  f  i punkten  ( x0, y0 ) .   Den ger ett mått på relativa förändringen av  f  i  y -led i punkten  ( x0, y0 ) .