2

 

 
Tangentplan och differentierbarhet
 

 
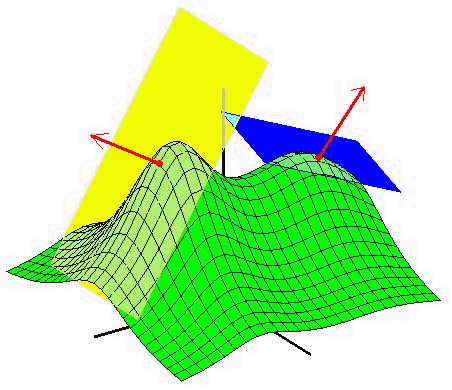
Ett plan genom en punkt  ( x0, y0, f( x0, y0))  på funktionsytan  z = f( x, y)  har en ekvation av formen
 
      z = f( x0, y0) + A1( x - x0) + A2( y - y0).
 
Om den relativa skillnaden mellan dessa båda uttryck går mot noll, för något val av  A = ( A1, A2) , när  ( x, y)( x0, y0)  är  f  differentierbar i  a . Planet med dessa konstanter  A1  och  A2  är då tangentplanet till  f  i punkten på funktionsytan.

 

 

 
Medelvärdessatsen i en variabel
 

 
Antag att  h ( t ) är en deriverbar funktion på intervallet  [ a, b ] .
 
Då finns det ett tal så att
  1. a <  <b
  2. h ( b ) - h ( a ) = h ' () ( b - a )