Riktningsderivata
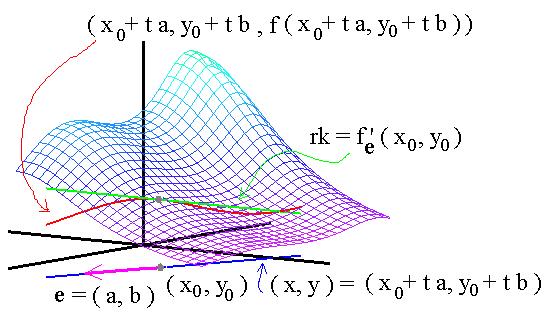
f 'v( x0, y0 ) = f 'x( x0, y0 ) a + f 'y( y0, y0 ) b = grad f ( x0, y0 )·v
|
Riktningsderivata |

|
|
Om f är kontinuerligt deriverbar och
v = ( a, b )
(där | v | = 1 )
kan
riktningsderivatan f 'v( x 0, y 0 ) beräknas som
f 'v( x0, y0 ) = f 'x( x0, y0 ) a + f 'y( y0, y0 ) b = grad f ( x0, y0 )·v |
|
Gradientens innebörd |
|
|
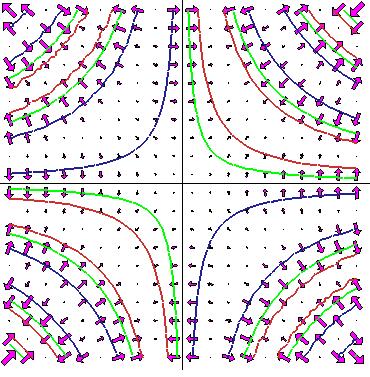
Funktionen är
f ( x, y ) = sin ( xy ).
I punkten
( x, y ) har
vektorn grad f = ( f 'x( ( x, y ) , f 'y( ( x, y ) ) markerats. |
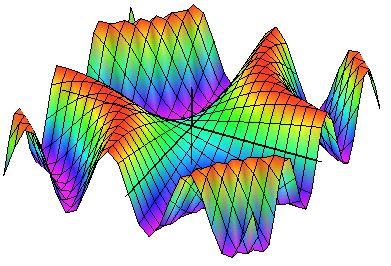
Så här ser grafen till funktionen ut
|
|
Gradienten och nivåyta |
|
|
|
|
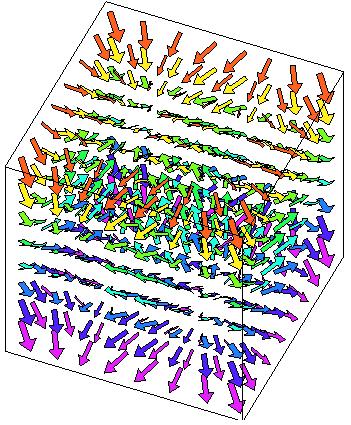
Figuren ovan visar gradientfältet grad f
till funktionen f ( x, y, z ) = sin ( x ) + sin ( y ) + sin ( z ) . |
|
|
|
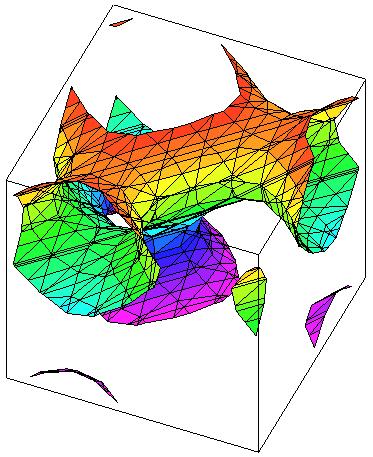
|
Figuren ovan visar nivåytan f ( x, y, z ) = 0.4 Försök obesrvera att gradienten i en punkt på ytan är vinkelrät mot ytan genom att jämföra figurerna. |