Lösningar Tentamen i MAN030 Flervariabelanalys, del 1, 02 06 12.
- Kedjeregeln ger
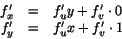
Ekvationen blir därför -yf'v=xy2-y, eller f'v=-u+1, som ger f=-uv+v+g(u), där g är en godtycklig deriverbar funktion.
Svar: f(x,y)=-xy2+y+g(xy), där g är en godtycklig deriverbar funktion. - Funktionen är kontinuerlig på den slutna begränsade ellipsskivan och
antar därför säkert ett största och ett minsta värde. Dessa antas när
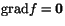 i det inre av skiva eller på skivans rand. Vi
söker stationära punkter i det inre och får ekvationssystemet
i det inre av skiva eller på skivans rand. Vi
söker stationära punkter i det inre och får ekvationssystemet
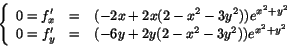
Efter förkortning med ex2+y2 (som ju är >0) får vi
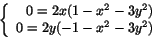
Översta ekvationen ger x=0 eller 1-x2-3y2=0. Första alternativet ger y=0 i nedersta ekvationen, medan det andra ger y=0 och därmed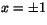 . De stationära punkterna är (0,0),
(-1,0) och (1,0) som samtliga ligger i det inre av ellipsskivan.
Vi har f(0,0)=2,
f(-1,0)=f(1,0)=e>2.
Längs randen till ellipsskivan, där
x2+3y2=2, har vi f=0
. De stationära punkterna är (0,0),
(-1,0) och (1,0) som samtliga ligger i det inre av ellipsskivan.
Vi har f(0,0)=2,
f(-1,0)=f(1,0)=e>2.
Längs randen till ellipsskivan, där
x2+3y2=2, har vi f=0
Svar: Största värdet är e och minsta är 0. - Vi ser att f är definierad (och kontinuerlig) över allt utom i
origo. Vi undersöker om f kan definieras även här så att den blir
kontinuerlig i hela planet. För kontinuitet ska vi ha att f(0,0) ska
vara gränsvärdet av f(x,y) när
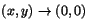 .
Vi har att
cos(t)=1-t2/2+t4B(t), där B är begränsad nära
t=0. Detta ger
.
Vi har att
cos(t)=1-t2/2+t4B(t), där B är begränsad nära
t=0. Detta ger
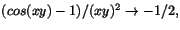 när
när
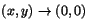 .
Polära koordinater ger att
.
Polära koordinater ger att
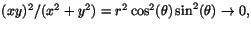 när
när
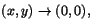 eftersom
eftersom
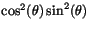 är begränsade.
Totalt får vi
är begränsade.
Totalt får vi
![$f=[(\cos(xy)-1)/(xy)^{2}][(xy)^{2}/(x^{2}+y^{2})\rightarrow
(-1/2)\cdot 0,$](img11.gif) när
när
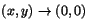 .
Vi har nu att f blir kontinuerlig i hela planet om vi sätter
f(0,0)=0.
Vi undersöker nu f när
.
Vi har nu att f blir kontinuerlig i hela planet om vi sätter
f(0,0)=0.
Vi undersöker nu f när
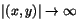 . Vi har
. Vi har
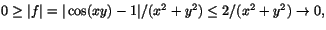 när
när
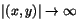 . Detta ger att f är likformigt
kontinuerlig.
. Detta ger att f är likformigt
kontinuerlig.
Svar: Funktionen f är likformigt kontinuerlig. - Enligt implicita funktionssatsen ger sambandet y som en funktion av
x och z i närheten av (1,2,1) om motsvarande gäller för
ekvationens linearisering kring punkten.
Sätter vi
g(x,y,z)=4x3z+z2y2-xy3 blir sambandet
0=g(x,y,z). Lineariseringen av detta är
0=g'x(1,2,1)(x-1)+g'y(1,2,1)(y-2)+g'z(1,2,1)(z-1). Vi har

så linearisering är 0=4(x-1)-8(y-2)+12(z-1). Eftersom vi kan lösa ut y som en funktion av x och z här kan vi också göra det i det ursprungliga sambandet (enligt implicita funktionssatsen). Löser vi ut y får vi y=x/2+3z/2, som är lineariseringen av y som funktion av x och z kring (1,1).
Svar: Lineariseringen är y=x/2+3z/2.
- Låt
v=(a,b), där a2+b2=1. För att bestämma
f'v(0,0) ska vi bestämma gränsvärdet av
(1/t)(f(ta,tb)-f(0,0))=(1/t)(tat2b2/(t2a2+t2b2))=ab2
när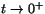 . Vi ser att detta uttryck är konstant så
f'v(0,0) existerar och är ab2.
Om nu f vore differentierbar i (0,0) skulle vi kunna beräkna
riktningsderivator med hjälp av kedjeregeln:
. Vi ser att detta uttryck är konstant så
f'v(0,0) existerar och är ab2.
Om nu f vore differentierbar i (0,0) skulle vi kunna beräkna
riktningsderivator med hjälp av kedjeregeln:
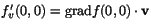 .
Vi har (enligt ovan)
f'x(0,0)=f'(1,0)(0,0)=0 och
f'y(0,0)=f'(0,1)(0,0)=0, som ger
.
Vi har (enligt ovan)
f'x(0,0)=f'(1,0)(0,0)=0 och
f'y(0,0)=f'(0,1)(0,0)=0, som ger
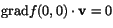 . Detta strider mot beräkningarna ovan. Alltså är f inte
differentierbar i origo.
. Detta strider mot beräkningarna ovan. Alltså är f inte
differentierbar i origo.
Svar: Funktionen är inte differentierbar i origo.
Jan-Alve Svensson
2002-06-12