Lösningar Tentamen i MAN030 Flervariabelanalys, del 1,
02 08 12.
- Kedjeregeln ger
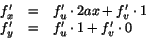
Väljer vi a=1/2 blir ekvationen därför f'v=y=u-v2/2, som ger f=uv-v3/6+g(u), där g är en godtycklig deriverbar funktion. Återgång till variablerna x och y ger f(x,y)=(x2/2+y)x-x3/6+g(x2/2+y), vilket i sin tur ger f(x,0)=x3/3+g(x2/2) som alltså ska vara x2+x3/3. Detta leder till g(x2/2)=x2. Sätter vi t=x2/2 har vi x2=2t och g(t)=2t. Den sökta lösningen är alltså f(x,y)=(x2/2+y)x-x3/6+2(x2/2+y)=x3/3+x2+xy+2y.
Svar: f(x,y)=(x2/2+y)x-x3/6+g(x2/2+y), där g är en godtycklig deriverbar funktion respektive f(x,y)=(x2/2+y)x-x3/6+2(x2/2+y)=x3/3+x2+xy+2y. - Funktionen är kontinuerlig på den triangelskivan säm är sluten
och begränsad och därmed kompakt. Fuy ktionen antar därför säkert
ett största och ett minsta värde. Dessa antas när
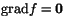 i det inre av skivan eller på skivans rand. Vi söker
stationära punkter i det inre och får ekvationssystemet
i det inre av skivan eller på skivans rand. Vi söker
stationära punkter i det inre och får ekvationssystemet
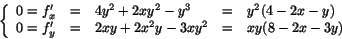
Den andra ekvationen ger x=0, y=0 eller 8-2x-3y=0. Första fallet ger y=0 eller y=4 i första ekvationen. Men (0,0) och (0,4) ligger inte i det inre av skivan. Fallet y=0 ger x godtyckligt i första ekvationen, men ingen punkt (x,0) ligger i det inre av skivan. Fallet 8-2x-3y=0 tillsammans med 4-2x-y=0 från första ekvationen ger y=2 och x=1 och (1,2) ligger i det inre av skivan. Där har vi f(1,2)=4. Vi undersöker nu f längs skivans rand. Den består för det första av punkter (t,0), för det andra av (0,t) och för det tredje av (6-t,t) där t varierar mellan 0 och 6. Vi har f(t,0)=0=f(0,t) och längs den tredje delen av randen f(6-t,t)=4(6-t)t2-(6-t)2t2-(6-t)t3=2t3-12t2. Derivering av detta ger 6t2-24t som är 0 när t=0 och när t=4. Bara det andra värdet är intressant. Vi har f(6-4,4)=f(2,4)=-64.
Svar: Största värdet är 4 och minsta är -64. - Vi ska ha att
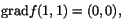 vilket ger systemet
vilket ger systemet
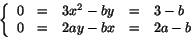
som ger b=3 och a=3/2. Där med är f=x3+3y2/2-3xy. För att avgöra vilket typ av stationär punkt (1,1) är ska vi undersöka den kvadratiska formen Q=f''xx(1,1)h2+2f''xy(1,1)hk+f''yy(1,1)k2. Vi har
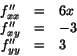
så Q=6h2-6hk+3k2=6(h-k/2)2+(3-6/4)k2, som är positivt definit. Punkten (1,1) är därför en lokal minimipunkt.
Svar: a=3/2, b=3 och (1,1) är en lokal minimipunkt till funktionen. - För att bestämma f'x(0,0) och fy(0,0) ska vi beräkna
gränsvärdet av
(f(t,0)-f(0,0))/t=0/t=0 respektive (f(0,t)-f(0,0))/t=0/t=0 när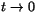 . Båda gränsvärdena
existerar och är 0.
Om f vore differentierbar i origo skullen den även vara kontinuerlig
där. Men f(0,0)=0 och
f(t,t2)=1/2, när
. Båda gränsvärdena
existerar och är 0.
Om f vore differentierbar i origo skullen den även vara kontinuerlig
där. Men f(0,0)=0 och
f(t,t2)=1/2, när 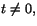 så f
antar värdena 0 och 1/2 i varje omgivning till origo och kan
därför inte vara kontinuerlig där.
så f
antar värdena 0 och 1/2 i varje omgivning till origo och kan
därför inte vara kontinuerlig där.
Svar: f är inte differentierbar. - Funktionen är kontinuerlig över allt där den är definierad eftersom
den är kvot av två kontinuerliga uttryck. Den är inte definierad längs
enhetscirkeln.
Området
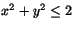 är kompakt och f är kontinuerlig där och
därför likformigt kontinuerlig. Allstå är den det även på det mindre
området
x2+y2<1/2.
Om f vore likformigt kontinuerlig på x2+y2<1 skulle den ha
en kontinuerlig utvidgning till randen som är enhetscirkeln.
Vi undersöker f då
är kompakt och f är kontinuerlig där och
därför likformigt kontinuerlig. Allstå är den det även på det mindre
området
x2+y2<1/2.
Om f vore likformigt kontinuerlig på x2+y2<1 skulle den ha
en kontinuerlig utvidgning till randen som är enhetscirkeln.
Vi undersöker f då
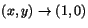 . Längs x-axeln har vi
f(x,0)=
. Längs x-axeln har vi
f(x,0)=
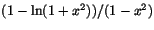 . När
. När
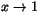 går täljaren
mot
går täljaren
mot
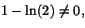 medan nämnaren går mot 0. Funktionen f har
alltså inget gränsvärdet när (x,y) går mot (1,0) och kan därför
inte utvidgas kontinuerligt till denna punkt. Funktionen är alltså
inte likformigt kontinuerlig i området x2+y2<1.
medan nämnaren går mot 0. Funktionen f har
alltså inget gränsvärdet när (x,y) går mot (1,0) och kan därför
inte utvidgas kontinuerligt till denna punkt. Funktionen är alltså
inte likformigt kontinuerlig i området x2+y2<1.
Svar: Funktionen är likformigt kontinuerlig i x2+y2<1/2, men inte i x2+y2<1.
Jan-Alve Svensson
2002-08-13