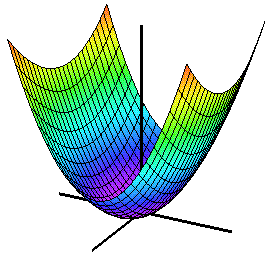
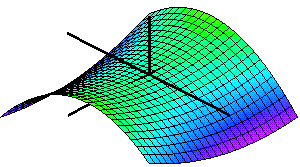
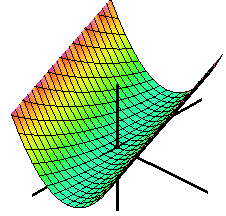
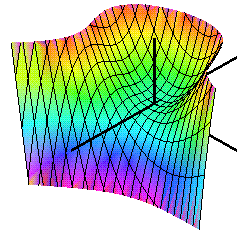
|
Extrempunkter |
|
|
Grafen till en funktion f över ett slutet begränsat område
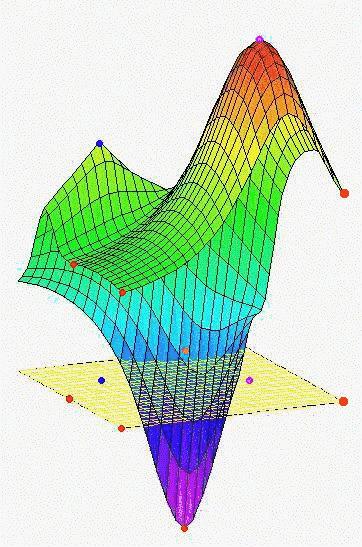
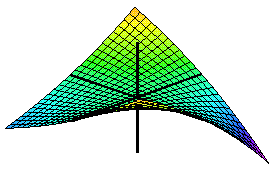
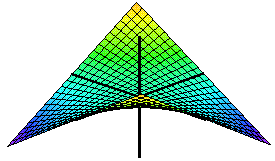
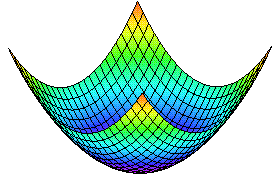
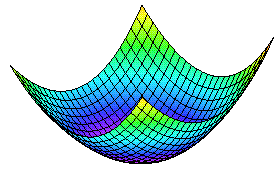
i x, y- planet. Funktionen har fyra extremvärden i punkter på randen till området. Den har två extremvärden i punkter i det inre av området. I den ena (kritisk punkt) är funktionen inte deriverbar, i den andra har funktionen en stationär punkt (kritisk punkt). |
|
Kvadratiska former |
|
|
|
|
Den kvadratiska formen x 2 + 3 y 2 (positivt definit). |
Den kvadratiska formen x 2 + x y - 3 y 2 (indefinit). |
|
|
|
Den kvadratiska formen x 2 -6 x y + 9 y 2 (positvt semidefinit). |
Funktionen 2(x 2 -6 x y + 9 y 2) - ( 3 x + y ) 3 har den till vänster som associerad kvadratisk form. |
|
Ett exempel på extrempunkter |
|
|
|
|
Grafen till funktionen
f ( x, y ) = x y e y - x. Funktionen har stationära punkter i ( 0, 0 ) och ( 1, -1 ). |
|
|
|
| Grafen kring punkten ( 0, 0 ). | Q ( x, y ) = 2 x y kring ( 0, 0 ). |
|
|
| Grafen kring punkten ( 1, -1 ). | Q ( x, y ) = e -2 ( x 2 + y 2) kring ( 0, 0 ). |