
Dugga 3 i MAN030 Flervariabelanalys del 1,
03 03 07, kl 10.00-10.30.
- Avgör om det finns en omgivning till (0,1), där funktionen
f(x,y)=(x3y2+xy-1,xy3+x2y+1)
är inverterbar.
- Visa att man i ekvationssystemet
i närheten av lösningen (1,1,1) kan uttrycka x och z som
funktioner av y.
- Finns det någon kontinuerlig funktion f på
- D=[0,1] sådan att
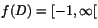 ?
?
- D=]0,1] sådan att
![$f(D)=[-1,0[\cup]0,1]$](img5.gif) ?
?
- D=]0,1[ sådan att
f(D)=R?
Ange i så fall en sådan funktion eller ge ett motiv till att den inte finns.
JAS
Jan-Alve Svensson
2003-03-07
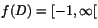 ?
?![$f(D)=[-1,0[\cup]0,1]$](img5.gif) ?
?