$\parbox{9cm}{MATEMATIK \\ Göteborgs universitet\\ \\ Skriv namn på varje inlämnat papper \\ }$ $\parbox{3cm}{Hjälpmedel: inga.}$

Dugga 3 i MAN 030 Flervariabelanalys, del 1, 02 03 08, kl 10.00-10.30.

1.

Avgör (argument krävs!) om talföljden (x_k) är konvergent eller divergent när

(a)

$x_{k}=\sin(k)/k,$

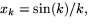
(b)

$x_{k}=k\cos(1/k)$.

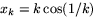2.

Avgör (argument krvävs!) om mängden M är kompakt när

(a)

$M=\{(x,y): \cos(x)+\cos(y)=1\},$

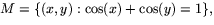
(b)

$M=\{(x,y): 1\leq 2-x^{2}-y^{2}<3\}$.

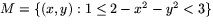3.

Motivera (inte i detalj) att funktionen f(x,y)=2+2x-x²-y² antar ett största och ett minsta värde på mängden 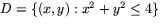$D=\{(x,y): x^{2}+y^{2}\leq 4\}$. Bestäm f(D).

JAS
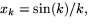
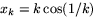
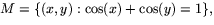
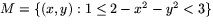