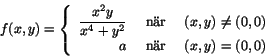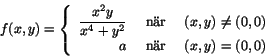
Dugga 1 i MAN 030 Flervariabelanalys, del 1,
03 02 07, kl 10.00-10.30.
- Bestäm en ekvation för tangentplanet till grafen av
f(x,y)=x2+xy,
i den punkt där x=1 och y=2.
- Avgör om mängden
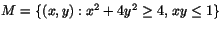 är öppen, sluten eller varken
öppen eller sluten. Är den begränsad? (Argument krävs!)
är öppen, sluten eller varken
öppen eller sluten. Är den begränsad? (Argument krävs!)
- Går det att bestämma konstanten a så att funktionen
är kontinuerlig i origo?
JAS
Jan-Alve Svensson
2003-02-10