![]()
Svar: f(x,y)=y+(1-xy/(2y-2x))2.
Största och minsta värdet antas i en punkt som löser ekvationssystemet
![]()
Den andra ekvationen kan uttryckas:
![]()
![]()
Svar: Stösta värdet är 9 och minsta är -9.
Vi har f''xx(-y-y+xy)e-x-2y, f''yx=(1-x-2y+2xy)e-x-2y och f''yy=(-2x-2x+4xy). För att avgöra om de stationära punkterna är extrempunkter undersöks den kvadratiska formen f''xxh2+2f''yxhk+f''yyk2.
I (0,0) är den 2xy som är indefinit (positiv i (1,1), negativ i t.ex. (-1,1)). Alltså en sadelpunkt och ingen extrempunkt.
I (1,1/2) är den e-2(-k2/2-2h2), som är negativt definit. Alltså ett lokalt maximum.
Svar: Enda extrempunkten är (1,1/2).
![]()
![]()
Talet f''xy(0,0) är gränsvärdet av
(f'y(x,0)-f'y(0,0))/x=1 när ![]()
- (a)
- Vi har
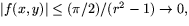 när
när
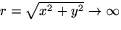 . Funktionen är dessutom
kontinuerlig på den slutna mängden
. Funktionen är dessutom
kontinuerlig på den slutna mängden 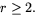 Detta ger att f är
likformigt kontinuerlig när
Detta ger att f är
likformigt kontinuerlig när 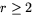 och därför även när r>2.
och därför även när r>2.
- (b)
- Om f vore likformig på r>1 skulle den ha en kontinuerlig
utvidgning till
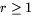 . Speciellt skulle den ha ett gränsvärde
när
. Speciellt skulle den ha ett gränsvärde
när 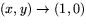 .
.Vi har
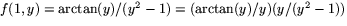 . När
. När
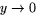 gäller att
gäller att 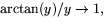 men
men
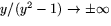 . Detta betyder att f saknar
gränsvärde när
. Detta betyder att f saknar
gränsvärde när 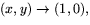 och kan därför inte
utvidgas kontinuerligt till området
och kan därför inte
utvidgas kontinuerligt till området 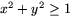 .
.