lsnMAN030a030324

Lösningar Tentamen i MAN030 Flervariabelanalys, del 1, 03 03 24.
3.	Mängen D som bestäms av $x^{2}+y^{2}\leq 1,$ $0\leq x$ är kompakt och funktionen är kontinuerlig på mängden. Den antar därför säkert ett största och ett minsta värde på mängden. Detta inträffar längs randen eller i stationära punkter i det inre av mängden. För stationära punkter löses $\begin{displaymath} \left\{ \begin{array}{lclcl} 0&=&f'_{x}&=&2x(y-1)\\ 0&=&f'_{y}&=&x^{2}-5y^{2} \end{array}\right. \end{displaymath}$ Den första ekvationen ger x=0 eller y=1 som ingedera kan leda till inre punkt i mängden D. Stationära punkter i det inre saknas. Vi undersöker f längs den del av randen där x²+y²=1, $x\geq 0$ . Uttrycket för den förenklas där till f=g(y)=y-8y³/3-1+y², där $-1\leq 1$ . Man har 0=g'(y), när y=1/2, y=-1/4. 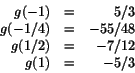Detta ger de intressanta värdena $\begin{displaymath} \begin{array}{rcr} g(-1)&=&5/3\\ g(-1/4)&=&-55/48\\ g(1/2)&=&-7/12\\ g(1)&=&-5/3 \end{array} \end{displaymath}$ Längs den andra delen av randen är x=0 och $-1\leq y\leq 1$ . Funktionen förenklar där till h(y)=f=-5y³/3 som är strängt avtagande. Eftersom g(1)=h(1) och g(-1)=h(-1) blir funktionen största värde 5/3 och det minsta blir -5/3. Svar: 5/3 respektive -5/3.
4.	Variabelbytet ger $\begin{displaymath} \begin{array}{rcr} f'_{x}&=&f'_{u}\cdot a+f'_{v}\cdot 1\\ f'_{y}&=& f'_{y}\cdot b+f'_{v}\cdot 0. \end{array} \end{displaymath}$ Väljer man a=1 och b=-2 får man att 2f'_x+f'_y=f'_v, så att ekvation blir f'_v=0. Detta ger f=g(u), där g är en godtycklig deriverbar funktion. Detta ger f(x,y)=g(x-2y). Man ska ha x²=f(x,0)=g(x-0)=g(x), så f(x,y)=(x-2y)². Svar: f(x,y)=g(x-2y), där g är en godtycklig deriverbar funktion. Den speciella funktionen är f(x,y)=(x-2y)².
5.	Extrempunkter är stationära punkter eftersom funktionen är differentierbar. Dessa löser $\begin{displaymath} \left\{ \begin{array}{rcl} 0&=&-2x+(y/2-1)(y^{2}-x^{2})\\ 0&=&2y+(x/2-1)(y^{2}-x^{2}) \end{array}\right. \end{displaymath}$ Skilnaden mellan dessa ekvationer blir 0=(y+x)(2+(y-x)(x/2-y/2)), som ger y=-x eller $y=x\pm 2$ . Första fallet ger x=0 i första ekvationen, fallet y=x-2 ger i andra ekvationen 0=2x-4+(x/2-1)(-4x-4), som ger $x=\pm 2$ . Fallet y=x+2 ger i andra ekvatione 0=2x+4+(x/2-1)(4x+4), dvs x=0. Totalt är de stationära punkterna (0,0), (2,0) och (0,2). 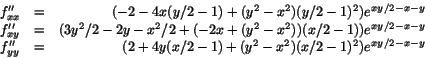Man har $\begin{displaymath} \begin{array}{rcr} f''_{xx}&=& (-2-4x(y/2-1)+(y^{2}-x^{2}... ...(2+4y(x/2-1)+(y^{2}-x^{2})(x/2-1)^{2})e^{xy/2-x-y}\end{array} \end{displaymath}$ I (0,0) är den kvadratiska formen Q=-2h²+2k², som är indefinit. Sadelpunkt. I (0,2) är Q=-2e^-2(h²-2hk+k²)=-2e^-2(h-k)² som är negativt semidefinit. I (2,0) är Q=2e^-2(h²-2hk+k²)=2e^-2(h-k)² som är positivt semidefinit. I de två sista punkterna fungerar inte metoden med kvadratisk form. Vi gör variabelbytet $\begin{displaymath} \left\{ \begin{array}{rcl} u&=&y+x\\ v&=&y-x \end{array}\right. \end{displaymath}$ Funktionen blir då f=uve^{(u²-v²)/8-u}=ue^u²/8-uve^-v²/8=g(u)h(v), där g(u)=ue^u²/8-u och h(v)=ve^-v²/8. Vi har g'=(1+u²/4-u)e^u²/8-u, eller g'=(1-u/2)²e^u²/8-u som är >0 utom när u=2. Funktionen g är därför strängt växande. Detta visar att f saknar extrempunkter. Svar: Extrempunkter saknas.
6.	Linearisering av ekvationen kring lösningen (1,2,0) ger 4(x-2)+8(y-1)+7z=0, där z kan lösas ut som funktion av x och y. Enligt inversa funktionssatsen är detta möjligt även i den ursprungliga ekvationen i närheten av (2,1,0). Vi ser att (1,2,z) löser ekvationen. Så inte i någon omgivning (1,2,0) kan ytan framställas som grafen till en funktion av x och y.
7.	För differentierbarhet krävs kontinuitet. Eftersom $\begin{displaymath} \frac{\sin xy}{\sqrt{x^{2}+y^{2}}}=\frac{\sin xy}{xy}\frac{xy}{\sqrt{x^{2}+y^{2}}}\rightarrow 1\cdot0=0, \end{displaymath}$ när $(x,y)\rightarrow(0,0)$ ska a=0 för kontinuitet. (Vi har använt att $\sin t/t\rightarrow 1,$ när $t\rightarrow 0$ och att $\begin{displaymath} \frac{xy}{\sqrt{x^{2}+y^{2}}}=\left\{\mbox{ PK }\right\}=r\cos t\sin t\rightarrow 0, \end{displaymath}$ oberoende av t, när $r\rightarrow 0$ .) Eftersom f då är konstant 0 längs axlarna är den partiellt deriverbar i origo med partialderivator båda =0. För att avgöra differentierbarhet ska vi undersöka det relativa felet $\begin{displaymath} R(x,y)=\frac{1}{\sqrt{x^{2}-y^{2}}}\Big(\frac{\sin xy-0}{\sqrt{x^{2}+y^{2}}}-(0,0)\cdot(x,y)\end{displaymath}$ när $(x,y)\rightarrow(0,0)$ . Polära koordinater och samma trick som ovan ger $\begin{displaymath} R=\frac{\sin xy}{\sqrt{x^{2}+y^{2}}}\cos t\sin t \end{displaymath}$ som saknar gränsvärde oberoende av t när $(x,y)\rightarrow(0,0)$ .
8.	Eftersom $\arctan t/ t\rightarrow 1,$ när $t\rightarrow 0$ har vi $f=(\arctan x^{2}y /x^{2}y)(x^{2}y /\sqrt{x^{2}+y^{2}})\rightarrow 1\cdot 0=0,$ när $(x,y)\rightarrow (0,0),$ (eventuellt med hjälp av polära koordinater). Vi kan därför utvidga f kontinuerligt till origo genom att sätta f(0,0)=1. Vidare gäller att $\vert f\vert\leq \pi/2(x^{2}+y^{2})\rightarrow 0,$ när $\vert(x,y)\vert\rightarrow \infty$ . Detta ger att f är likformigt kontinuerlig.

Jan-Alve Svensson
2003-03-24