| 1. |
Sätter vi
f (x, y, z) = xz2 + x2y2 + y3z ges en normal till
tangentplanet av
gradf (1, 2, 3). Vi har
gradf = (z2 + 2xy2, 2x2y + 3y2z, 2xz + y3), så
(17, 40, 14) är en normal. Tangentplanet har därför ekvationen
0 = (17, 40, 14) . (x - 1, y - 2, z - 3).
Svar: 139 = 17x + 40y + 14z.
| ||||||||||
| 2. |
Området är slutet och begränsat och därmed kompakt. Eftersom
funtkionen är kontinuerlig antar den därför ett störtsta och ett
minsta värde i området.
Eftersom
x, y, z Vi söker stationära punkter till f. Där är gradf = x-1/2y-1/2(yz/2, xz/2, xy) = (0, 0, 0), vilket inträffar precis när minst två av koordinaterna är = 0. Ingen sådan punkt är en inre punkt i området, så största värdet antas längs randen på området.
Randet består av tre trianglar i olika koordinatplan där f antar
värdet 0 och triangelytan i planet
x + 2y + 3z = 4, där
x, y, z Sätter vi g(x, y, z) = x + 2y + 3z gäller att största värdet antas i en punkt som löser
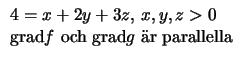
Det sista villkoret kan skrivas (0, 0, 0) = x-1/2y-1/2(yz/2, xz/2, xy)×(1, 2, 3), dvs
(0, 0, 0) = x-1/2y-1/2(3xz/2 - 2xy, - 3yz/2 + xy, yz - xz/2),
som tillsammans med det första villkoret ger 3z = 4y, 3z = 2x och
x = 2y. Insatt i den första ekvationen ger detta 4 = 3x, eller
x = 4/3, y = 2/3, och z = 8/9. Vi har
f (4/3, 2/3, 8/9) = 2
Svar: Största värdet är
16
| ||||||||||
| 3. |
Det stationära punkterna till f (x, y) löser ekvationssystemte
Den översta ekvationen ger x = 0 eller x = - 2y som i den nedre ger y = 0 respektive y = 0, y = 1, eller y = 1/2. De stationära punkterna är alltså (0, 0), (- 2, 1) och (- 1, 1/2). Vi undersöker respektive kvadratisk form associerad till dessa punkter. Vi har
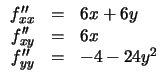
I (0, 0) ger detta den kvadratiska formen -4k2 som är negativt semidefinti och därför inte kan användas för att avgöra om origo är en lokal extrempunkt. Däremot är f (x, 0) = x3, så vi ser att origo inte är en lokal extrempunkt. I (- 2, 1) är den kvadratiska formen -6h2 - 24hk - 28k20 = - 6(h + 2k)2 - 4k2, som är negativt definit. Allstå är (- 2, 1) en lokal maximipunkt. I (- 1, 1/2) är den kvadratiska formen -3h2 - 12hk - 10k20 = - 3(h + 2k)2 + 2k2 som är indefinti. Punkter är därför en sadelpunkt. Svar: De stationära punkterna är (0, 0), (- 2, 1) och (- 1, 1/2) och bara (- 2, 1) är en lokal extrempunkt.
| ||||||||||
| 4. |
| ||||||||||
| 5. |
För differentierbarhet krävs kontinuitet. Detta ger att vi måste
välja
a =
f (x, 0) =
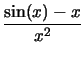 = - x/(3!) + x3B(x), = - x/(3!) + x3B(x),
där B(x) är begräsad nära x = 0. Detta ger a = 0, som enda möjlighet. För differentierbarhet i origo krävs att de partiella derviatorna där ska existera. Vi har
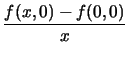 = - 1/6 + x2B(x) = - 1/6 + x2B(x)
R(x, y) =
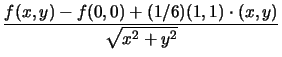
går mot noll när
(x, y) Vi har
R(x, y) =
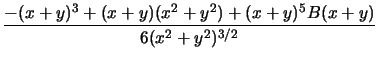
Övergång till polära koordinater ger att vi kan strunta i termen med B och att vi då får
- (cos t + sin t)3/6 + (cos t + sin t)/6
som inte har något gränsvärde oberoende av t när
r = Svar: Nej.
| ||||||||||
| 6. |
Vi vet att
f är differentierbar som en följd av
förutsättningarna och har därför att
R(b) =
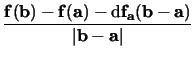
går mot
0, när
b Vi sätter b = a + th (t > 0) och får av detta . Efter skalärprodukt med th och division med t2, att
0
enligt förutsättnigen. När
t |