Differentierbarhet och kontinuitet
|
| 1 |
Bestäm, om möjligt talet a, så att
Blir kontinuerlig. Motivera! Blir f(x,y)
då också differentierbar i (0,0)?
|
| 2 |
| a) |
Ange den precisa matematiska definitionen av att
f(x) är partiellt deriverbar i a
(en inre punkt i f:s
definitionsmängd). |
| b) |
Är funktionen
partiellt deriverbar i (0,0)? |
| c) |
Ange den precisa matematiska definitionen av att f(<I>x)
är differentierbar i <I>a (en inre punkt i f:s
definitionsmängd). |
| d) |
Är funktionen i b)
differentierbar i (0,0)?
|
|
| 3 |
Avgör om funktionen
är differentierbar.
|
Öppna, slutna och kompakta mängder
|
| 4 |
Avgör om följande påståenden är sanna eller falska. Motivera
ordentligt!
| a) |
Om den reellvärda funktionen f(t) är kontinuerlig, så är
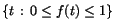 kompakt. kompakt. |
| b) |
Mängden
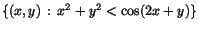 är öppen och
begränsad. är öppen och
begränsad. |
| c) |
Mängden
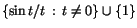 är sammanhängande. är sammanhängande.
|
|
| 5 |
Skissa följande delmängder till planet. Avgör för var och en av
dem om den är öppen, sluten, begränsad respektive kompakt
(motivering krävs inte!).
|
Kedjeregeln och partiella differentialekvationer
|
| 6 |
Lös differentialekvationen
f'x-xf'y=y t.ex. genom att
göra variabelbytet u=ax2+y, v=x för lämplig konstant
a. Bestäm också den lösning f sådan att
f(x,0)=x2+x3/3.
|
| 7 |
Lös differentialekvationen
x2f'x+y2f'y t.ex. genom
variabelbytet u=1/x-1/y och v=1/y.
|
| 8 |
Man vill bestämma en kontinuerligt deriverbar funktion f(x,y), så att nivåkurvorna till
denna skär nivåkurvorna till g(x,y)=xy rätvinkligt. Hur ska
f se ut (bestäm alla möjliga lösningar)? Man kan ha nytta av
variabelsubstitutionen
u=x2-y2, v=xy.
|
Tangentplan och riktningsderivata
|
9 |
Bestäm ekvationen för tangenlinjen till kurvan
x2+xy+2y2=1 i punkten (1,0).
|
10 |
Visa att
fv(0,0) existerar och bestäm dess värde
när
och v bestäms av (1,1).
Avgör om f(x,y) är differentierbar i origo.
|
11 |
Bestäm en ekvation för tangentplantet till ytan
x3+4x2y+y=z2 i punkten (1,0,1).
|
12 |
Betäm riktningsderivatan till
f(x,y)=x2-xy2+y3 i (1,1) i den riktning som ges av
(3,4).
|
13 |
Ytorna
x2+y2-z2=2 och x+y-2ez=0 skär varandra i en
kurva genom (1,1,0). Bestäm en ekvation för tangentlinjen till
kurvan i denna punkt.
|
Taylorutveckling och lokala extemvärden
|
14 |
Bestäm de lokala extrempunkterna till
f(x,y)=xye-x-2y.
|
15 |
Bestäm Taylorpolynomet av ordning två till
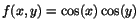 kring punkten kring punkten 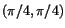 . .
|
16 |
Bestäm de stationära punkterna till
f(x,y)=x2+2xy+xy2
och avgör deras karaktär.
|
17 |
Bestäm de stationära punkterna till
f(x,y)=x2-x2y+2y2
och avgör deras karaktär.
|
18 |
Punkten
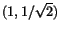 är en stationär punkt till är en stationär punkt till
Avgör om det är en lokal
extrempunkt.
|
Linjär approximation, inversa och implicita
funktionssatsen
|
| 19 |
Visa att sambandet
xey+yez+zex=1 definierar z som
en differentierbar funktion i en omgivning till (0,1,0) Bestäm
z'x(0,1) och z'y(0,1).
|
| 20 |
Visa att sambandet
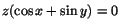 definierar z som en
funktion av x och y i närheten av (0,0,0), men inte i närheten
av definierar z som en
funktion av x och y i närheten av (0,0,0), men inte i närheten
av
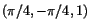 . .
|
Avbildningsegenskaper hos kontinuerliga funktioner
|
| 21 |
Undersök i vart och ett av fallen nedan om det finns en
kontinuerlig funktion f så att f(S)=D, när
| a) |
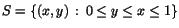 och och
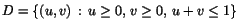
|
| b) |
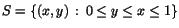 och och
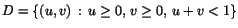
|
| c) |
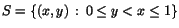 och och
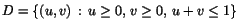
|
| d) |
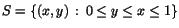 och och
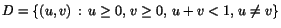
|
|
| |
Ange i förekommande fall en sådan funktion.
|
| 23 |
Låt
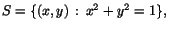
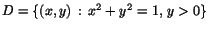 och och
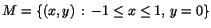 . Undersök om det finns kontinuerliga funktioner som
uppfyller följande villkor och ange i förekommande fall en sådan. . Undersök om det finns kontinuerliga funktioner som
uppfyller följande villkor och ange i förekommande fall en sådan.
a) D=f(S) b) 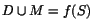 c) c) 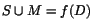 d)
CS=f(CD), där CS är komplementet till
S. d)
CS=f(CD), där CS är komplementet till
S.
|
Likformig kontinuitet
|
| 22 |
Avgör om funktionen 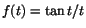 är likformigt kontinuerlig
på intervallet är likformigt kontinuerlig
på intervallet ![$]0,\pi/4]$](img31.gif) . .
|
| 24 |
Visa att 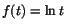 är likformigt kontinuerlig på är likformigt kontinuerlig på ![$]r,\infty[,$](img33.gif) för varje r>0, men inte på
för varje r>0, men inte på ![$]0,\infty[ $](img34.gif)
|
Optimering
|
| 25 |
Bestäm det största värde som f(x,y)=x2y antar på
ellipsen
x2+2y2=1.
|
| 26 |
Motivera att funktionen
f(x,y)=4xy2-x2y2-xy3 har ett
största och ett minsta värde i triangelytan med hörn i (0,0),
(6,0) och (0,6). Bestäm dessa värden!
|
| 27 |
Motivera att funktionen f(x,y)=xy antar ett största och ett
minsta värde i det området i planet där
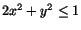 . Bestäm
dessa värden. . Bestäm
dessa värden.
|
| 28 |
Motivera att
f(x,y)=(x+y)/(1+x2+y2) har ett största och
ett minsta värde i området som ges av
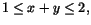 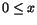 och
och 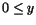 . Bestäm också dessa värden. . Bestäm också dessa värden.
|
| 29 |
Motivera att funktionen
f(x,y)=xy2e-x2-y2 har ett
största och ett minsta värde i området där
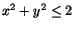 och och
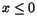 . Bestäm dessa värden! . Bestäm dessa värden!
|
| 30 |
Ett företag har två fabriker som producerar kvantieterna q1
respektive q2 av en vara. Den samanlagda kostnaden för
produktionen ges approximativt av
f(q1,q2)=2q12+q1q2+q2+500
och företaget vill producera 200 enheter av varan och samtidigt
minimera kostnaden för produktionen. Varför är problemet lösbart och
hur mycket ska respektive fabrik producera?
|
| 31 |
En biograf har olika biljettpriser för barn och vuxna eftersom
de anses olika priskänsliga. Man räknar med att sälja rpb-4
och spv-2 barn- respektive vuxenbiljetter när priserna sätts
till pb och pa. Biografens kostnader är proportionella
mot totala antalet sålda biljetter. Hur ska förhållandet mellan
priset på barn- och vuxenbiljetter vara för att biografen ska göra
största möjliga vinst. Varför är problemet lösbart?
|
| 32 |
Motivera att funktionen
f(x,y)=x3-y3 har ett största och
ett minsta värde på ellipsskivan
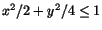 . Bestäm
också dessa värden. . Bestäm
också dessa värden.
|
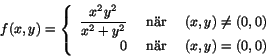
![]() c)
c) ![]() d)
CS=f(CD), där CS är komplementet till
S.
d)
CS=f(CD), där CS är komplementet till
S.
