
|
|
Tentamen i MAN030 Flervariabelanalys, del 1,
02 06 12, kl 8.45-13.45.
- Ange den precisa matematiska betydelsen av
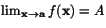 .
. - Ange den precisa matematiska definitionen av att f(x) är kontinuerlig i a.
- Visa att f är kontinuerlig i a om f är differentierbar i a.
- Ange den precisa matematiska betydelsen av
- Antag att f''xy och f''yx existerar och är kontinuerliga i en omgivning till (a,b). Visa att f''xy(a,b)=f''yx(a,b).
- Visa att en delmängd M till
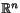 är kompakt precis när
varje punktföljd i M har en konvergent delföljd med gränsvärde i M.
är kompakt precis när
varje punktföljd i M har en konvergent delföljd med gränsvärde i M.
- Lös differentialekvationen xf'x-yf'y=xy2-y, t.ex. genom att göra variabelbytet u=xy, v=y.
- Motivera att funktionen
f(x,y)=(2-x2-3y2)ex2+y2 har
ett största och ett minsta värde i ellipsskivan
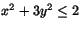 . Bestäm dessa värden!
. Bestäm dessa värden!
- Avgör om funktionen
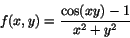
är likformigt kontinuerlig. Motivera noga! - Visa att sambandet xy3=4x3z+z2y2 bestämmer y som en funktion av x och z i närheten av punkten (1,2,1). Bestäm också lineariseringen av denna funktion kring punkten (1,1).
- Låt
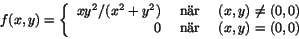
Visa att f'v(0,0) existerar för varje enhetsvektor v. Är f differentierbar i origo?
http://www.math.chalmers.se/Math/Grundutb/GU/MAN030/V02-1/Skrivningarna beräknas vara färdigrättade den 20 juni.
JAS
Jan-Alve Svensson
2002-06-12