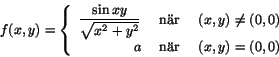Tentamen i MAN030, Flervariabelanalys 1, 03 03 24, kl 8.45-13.45.
1. Visa att en delmängd M till Rn är kompakt precis när varje punktföljd i M har en konvergent delföljd med gränsvärde i M.
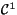2. Visa att om f(x,y) är en $\mathcal C^{1}$-funktion så är den differentierbar.
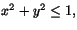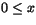3. Motivera att funktionen f(x,y)=y(x2-5y2/3)-x2 har ett största och ett minsta värde i området $x^{2}+y^{2}\leq 1,$ $0\leq x$. Bestäm också dessa värden.
4. Lös differentialekvationen 2f'x+f'y=0, t.ex. genom att göra ett variabelbyte av formen u=ax+by, v=x, för lämpliga konstanter a och b. Bestäm också den lösning som har f(x,0)=x2.
5. Berstäm de lokala extrempunkterna till funktionen

f(x,y)=(y2-x2)exy/2-x-y.

6. Visa att sambandet

(x3-1)z+(y-2)z3+x2y2=4

bestämmer z=z(x,y) som en funktion av x och y i närheten av (2,1,0). Bestäm också Taylorutvecklingen av ordning 1 av z(x,y) kring punkten (2,1). Är z en funktion av x och y i närheten av (1,2,0)?
7. Kan man bestämma konstanten a så att funktionen

\begin{displaymath}f(x,y)=\left\{ \begin{array}{rcl} \displaystyle{\frac{\si... ...q (0,0)\\ a&\mbox{ när }&(x,y)=(0,0)\\ \end{array}\right.\end{displaymath}

blir differentierbar i origo? Vad ska a i så fall vara?
8. Undersök om funktionen

\begin{displaymath}f(x,y)=\frac{\arctan x^{2}y}{x^{2}+y^{2}}\end{displaymath}

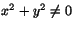är likformigt kontinuerlig i området där $x^{2}+y^{2}\neq 0$.
 

Jan-Alve Svensson
2003-03-24