MATEMATIK
Chalmers

Tentamen i MAN030, Flervariabelanalys 1, 03 04 15, kl 8.45-13.45.

1.

Visa att en delmängd M till Rⁿ är sluten precis när varje punktföljd i M som konvergerar har sitt gränsvärde i M.

2.

Visa att en differentierbar funktion är kontinuerlig.

3.

Bestäm en ekvation för tangentplanet till ytan

xz² + x²y² + y³z = 37

i punkten (1, 2, 3).

4.

Motivera att funktionen f (x, y, z) = x^1/2y^1/2z har ett största och ett minsta värde i det område i första oktanten ( x, y, z $\geq$ 0) där x + 2y + 3z $\leq$ 4. Bestäm också dessa värden.

5.

Bestäm de stationära punkterna till f (x, y) = x³ - 2y² - 2y⁴ + 3x²y och avgör om de är lokala extrempunkter.

6.

Vilken eller vilka av följande funktioner är likformigt kontinuerlig(a)? Motiv krävs!

(a)	f (t) = 1/cos t på [0,$\pi$/2[,
(b)	f (t) = cos(1/t) på [1, 2],
(c)	f (t) = t cos(1/t) på ]0, 2].

7.

Kan man bestämma konstanten a så att funktionen

f (x, y) = $$\left\{\vphantom{ \begin{array}{rcl} \displaystyle{\frac{\sin(x... ... (x,y)\neq (0,0)\\ a&\mbox{ n\uml {a}r }& (x,y)=(0,0) \end{array}}\right.$$$$\begin{array}{rcl} \displaystyle{\frac{\sin(x+y)-x-y}{x^{2}+y^{2... ... {a}r }& (x,y)\neq (0,0)\\ a&\mbox{ n\uml {a}r }& (x,y)=(0,0) \end{array}$$

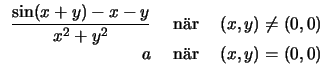
blir differentierbar i origo? Vad ska a i så fall vara? (Man kan ha användning för Maclaurin-utvecklingen sin(t) = t - t³/(3!) + t⁵/(5!) -....)

8.

Antag att f : Rⁿ $\rightarrow$ Rⁿ är en $\mathcal {C}$¹-funktion och att

(a - b) ^. (f(a) - f(b)) $$\leq$$ 0,

för alla a och b. Visa att då gäller att

h ^. df_a(h) $$\leq$$ 0,

för alla h. Här är df_a ( = f'(a) = df(a)) differentialen (eller (totala) derivatan) av f i punkten a.

Förslag till lösningar kommer att finnas på

http://www.math.chalmers.se/Math/Grundutb/GU/MAN030/V03-1/

Skrivningen beräknas vara färdigrättad måndagen den 28 april. Rättade skrivningar återfås på mottagningen i Matematiskt centrum. Öppet tider: vardagar 12.30 - 13.00. Resultat kan också fås per telefon: 772 5388.

JAS