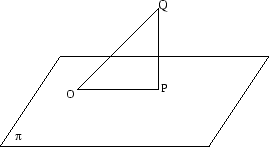
I figuren har vi också ritat ut origo, som ju ligger i planet!

I figuren har vi också ritat ut origo, som ju ligger i planet!
Den sökta punkten P=(x,y,z) ligger på linjen genom den givna punkten
Q=(1,1,1) och med normalen som riktningsvektor. Detta ger att
![]()
3x-4y+5z=3(1+3t)-4(1-4t)+5(1+5t) = 4+50t = 0
Alltså är t=-4/50 = -2/25. Sätter man in detta värde får man
x = 1+3(-2/25) = 0.76,
y = 1-4(-2/25) = 1.32,
z =
1+5(2/25) = 0.60
Innan man släpper lösningen måste man kontrollera varje steg!
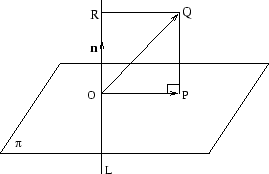
Hur räknar man ut den ortogonala projektionen av ![]() längs
normalen?
längs
normalen?
![]()
![]()
![]()
![]()
Här kommer ett problem där Q och P är givna medan ![]() söks och ett problem där P och
söks och ett problem där P och ![]() är givna medan Q
söks!
är givna medan Q
söks!
Extra uppgift 23 (b)
Man vet att punkten (0,1,2) är den punkt i ett plan ![]() som ligger
närmast
punkten (1,1,1). Vad kan sägas om
som ligger
närmast
punkten (1,1,1). Vad kan sägas om ![]() ?
?
Extra uppgift 23 (c)
Man vet att punkten (1,1,-1) är den punkt i planet x+2y+3z=0
som ligger närmast punkten Q. Vad kan sägas om Q?
(x,y,z)=(1,1,-1)+t(1,2,3)
En mängd av fyra vektorer, som är linjärt oberoende, bildar en bas i
ett
fyrdimensionellt rum.
De två vektorer som söks och de två som är givna skall alltså
tillsammans bilda en linjärt oberoende mängd!
Dags att tänka efter vad linjärt oberoende betyder! (Kolla i Lays
bok (sektion 1.6).
![]()
Detta innebär att ingen av de fyra vektorerna är en
linjärkombination av de andra tre! (Se sats 7 i Lays sektion 1.6.)
Om man har ett antal vektorer i ![]() kan man sätta dem
som kolonner i en matris A. Kolonnerna är då linjärt oberoende
om och endast om systemet
kan man sätta dem
som kolonner i en matris A. Kolonnerna är då linjärt oberoende
om och endast om systemet ![]() bara har den triviala
lösningen, vilket betyder att matrisen A har ett pivotelement i
varje kolonn! (Se Lays sektion 1.6)
bara har den triviala
lösningen, vilket betyder att matrisen A har ett pivotelement i
varje kolonn! (Se Lays sektion 1.6)
![]()
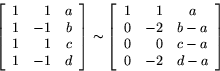
Vi har alltså massor av olika val! Låt oss då ta något enkelt! Vi tar
![]()
Denna metod ser ut att fungera!
Vi börjar med att sätta ![]() och försöker välja
och försöker välja
![]() så att systemet
så att systemet
![]()
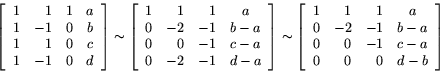
Hur vet vi nu att våra fyra vektorer
Sätter vi de fyra vektorerna som kolonner i en matris så får vi
(som kalkylen ovan visar) en matris som har en pivotelement i varje
kolonn. Kolonnerna är alltså en linjärt oberoende mängd
i
![]() ,
,![]() ,
,![]() och
och ![]() verkligen bildar en bas?
verkligen bildar en bas?
![]()
![]() . (Se Lays bok, sektion 1.6.)
. (Se Lays bok, sektion 1.6.)
Dessutom vet vi att fyra linjärt oberoende vektorer i
![]() bildar en bas. (Se Lays bok, sektion 2.9, Sats 15.)
bildar en bas. (Se Lays bok, sektion 2.9, Sats 15.)
Svar: ![]() är en bas
med de efterfrågade egenskaperna.
är en bas
med de efterfrågade egenskaperna.
Extra uppgift 29 (c)
Finn alla baser i ![]() som innehåller (1,1,1,1)
och (1,-1,1,-1).
som innehåller (1,1,1,1)
och (1,-1,1,-1).
Det finns också massor av likvärdiga (ekvivalenta) egenskaper!
Sats 7 i sektion 2.2 (som handlar om ekvationssystem),
sats 8 i sektion 2.3 (som handlar om ekvationssystem och matrisens
kolonner),
sats 4 i sektion 3.2 (som handlar om determinanter)
en sats om egenvärden i sektion 5.1.
Man kan bli knäckt för mindre!
En kvadratisk matris A är inverterbar om och endast om
ekvationssystemet ![]() bara har den triviala lösningen
bara har den triviala lösningen
![]() .
.
(Lay sektion 2.3, Sats 8 (d).)
En kvadratisk matris A är inverterbar om och endast om ![]() .
.
(Lay sektion 3.2, Sats 4.)
En kvadratisk matris A är inverterbar om och endast om talet 0
inte är ett egenvärde till A.
(Lay sektion 5.1, Satsen som föregår Sats 2.)
AC=A-A3=A(I-A2)
Sätt C=I-A2.
Då är AC=A(I-A2)=A-A3=I och CA=(I-A2)A=A-A3=I.
Alltså är A inverterbar med inversen C=I-A2.
![]()
Antag att A3 - A + I = 0 det vill säga A-A3=I.
Vi skall visa att A är inverterbar genom att beskriva dess
invers!
Antag att ![]() . Då gäller
. Då gäller ![]() .
.
Alltså är ![]() . Systemet
. Systemet ![]() har alltså endast den triviala lösningen! VSB.
har alltså endast den triviala lösningen! VSB.
Likheten I=A-A3 ger att ![]() .Produktformeln för determinter (Lay Sats 6 i sektion 3.2) ger att
.Produktformeln för determinter (Lay Sats 6 i sektion 3.2) ger att
![]()
OBS: Det är BIG ERROR att av skriva ![]() . Någon sådan räkneregel för determinater finns inte!
. Någon sådan räkneregel för determinater finns inte!
Låt ![]() vara ett egenvärde till A och
vara ett egenvärde till A och ![]() en motsvarande
egenvektor. Då är
en motsvarande
egenvektor. Då är ![]() och
och ![]() .
.
Eftersom ![]() får vi
får vi
![]()
Extra uppgift 30 (c)
En ![]() matris A har n olika egenvärden och uppfyller
ekvationen
A2-3A+2I=0. Vad
kan sägas om n?
matris A har n olika egenvärden och uppfyller
ekvationen
A2-3A+2I=0. Vad
kan sägas om n?