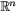
Inlämningsuppgift 3
Vilken eller vilka av följande delmängder S till  är
reguljära ytor? Ange en grafparametrisering kring punkten p när S
är en reguljär yta.
är
reguljära ytor? Ange en grafparametrisering kring punkten p när S
är en reguljär yta.
- 1.
- S ges av alla punkter (x,y,z) som löser ekvationen
x2y2+y2z2+x2z2+xyz=0. Punkten p är
(-1/3,-1/3,-1/3).
- 2.
- S ges av alla punkter (x,y,z) som löser ekvationen
x2y2+y2z2+x2z2+xyz=1. Punkten p är
(0,1,1).
- 3.
- S består av alla punkter (x,y,z) som löser ekvationssystemet

Punkten p är  .
. - 4.
- S är mängden av punkter (x,y,z) sådana att z3=x2+y2 och
p är (2,2,2).
- 5.
- S består av alla punkter

där  och
och  . (Observera att snittet
mellan S och planet Ax+By=0 består av disjunkta cirklar med
medelpunkt längs linjen genom origo i planet som är vinkelrät mot z-axeln.)
. (Observera att snittet
mellan S och planet Ax+By=0 består av disjunkta cirklar med
medelpunkt längs linjen genom origo i planet som är vinkelrät mot z-axeln.)
För 4 poäng krävs fullgod lösning av fyra av deluppgifterna.
Lösningarna ska lämnas senast fredagen den 11 februari.
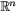
![]() är
reguljära ytor? Ange en grafparametrisering kring punkten p när S
är en reguljär yta.
är
reguljära ytor? Ange en grafparametrisering kring punkten p när S
är en reguljär yta.
![]()
![]()