
Inlämningsuppgift 4
- 1.
- Helikoiden är mängden av punkter
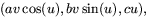 där
där
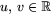 (och
(och 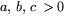 ). Visa att helikoiden är
inversa bilden av ett reguljärt värde till en glatt funktion, så att
den är en reguljär yta.
). Visa att helikoiden är
inversa bilden av ett reguljärt värde till en glatt funktion, så att
den är en reguljär yta.
- 2.
- Låt S1 vara den reguljära ytan
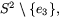 där S2 är enhetssfären och S2 helikoiden. Visa att
funktionen
där S2 är enhetssfären och S2 helikoiden. Visa att
funktionen
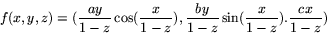
definierar en glatt funktion 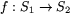 .
. - 3.
- Visa att en bas för tangentrummet T(x,y,z)(S1) ges av
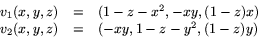
medan
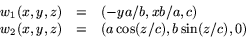
ger en bas för T(x,y,z)S2.
- 4.
- Vad är Jakobis matris för
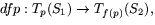 om
man använder baserna ovan och p=(0,1,0)?
om
man använder baserna ovan och p=(0,1,0)?
- 5.
- Är f en diffeomorfi?
För 4 poäng krävs fullgod lösning av fyra av deluppgifterna.
Lösningarna ska lämnas senast fredagen den 18 februari.
![]()
![]()
![]()

![]()
![]()
![]()