
Inlämningsuppgift 6
- 1.
- Visa att lösningarna till xy2-z=0 är en reguljär
orienterbar yta.
- 2.
- Välj en Gaussavbildning för ytan och bestäm dess Gauss- och
medelkrökning. Bestäm också vilka punkter på ytan som är elliptiska,
paraboliska respektive plana. Har ytan några navelpunkter?
- 3.
- Bestäm de asymptotiska linjerna på ytan.
- 4.
- Visa att
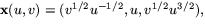 u,v>0, ger en parametrisering av ytan runt punkten (1,1,1),
sådan att koordinatkurvorna (
u,v>0, ger en parametrisering av ytan runt punkten (1,1,1),
sådan att koordinatkurvorna (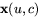 respektive
respektive 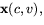 där c är en konstant) är asymptotiska linjer.
där c är en konstant) är asymptotiska linjer.
Lösningarna ska lämnas senast fredagen den 3 mars.
Jan-Alve Svensson
2/25/2000
