Lösning till MAN500, Differentialgeometri, 00 03 15.

1.

(a)

Välj en lokal parametrisering 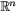$\alpha:I\rightarrow C,$ kring $p\in C,$ så att $\vert\alpha'\vert\equiv 1$ och $\alpha(0)=p$. Normalkrökningen ges då av $k_{n}(p)=\langle N,\alpha''\rangle$.

(b)

Välj en lokal parametrisering $\mathbf x:U\rightarrow S$ kring $p\in S,$ med $\mathbf x(q)=p$. Då är $\mathbf x_{u}(q),\,\mathbf x_{v}(q)$ en bas för T_p(S). För att visa att -dN_p är självadjungerad ska vi visa att $\langle-d_{p}Nv,w\rangle= \langle v,-d_{p}Nw\rangle,$ när $v,\,w\in T_{p}(S)$.

Vi skriver vektorerna i basen $\mathbf x_{u}(q),\,\mathbf x_{v}(q)$: $v=A\mathbf x_{u}(q)+B\mathbf x_{v}(q)$ och $w=C\mathbf x_{u}(q)+D\mathbf x_{v}(q)$.

Avbildningen -d_pN är linjär så $-d_{p}Nv=-Ad_{p}N\mathbf x_{u}(q)-Bd_{p}N\mathbf x_{v}(q)$ och $-d_{p}Nw=-Cd_{p}N\mathbf x_{u}(q)-Dd_{p}N\mathbf x_{v}(q)$. Sätter vi in detta i $\langle-d_{p}Nv,w\rangle= \langle v,-d_{p}Nw\rangle$ ser vi att det räcker att visa att

$$\langle d_{p}N\mathbf x_{u}(q),\mathbf x_{v}(q)\rangle =\langle \mathbf x_{v}(q), d_{p}N\mathbf x_{u}(q)\rangle .$$

Men $d_{p}N\mathbf x_{u}(q)=(N\circ x)_{u}(q)$ och $d_{p}N\mathbf x_{v}(q)=(N\circ x)_{v}(q)$ och $(\langle N\circ \mathbf x)(q)$ är vinkelrät mot såväl $\mathbf x_{u}(q)$ och $\mathbf x_{v}(q),$ så $\langle N\circ \mathbf x,\mathbf x_{u}\rangle \equiv \langle N\circ \mathbf x,\mathbf x_{v}\rangle \equiv 0$. Derivering med avseende på u av detta ger nu

$$0= \langle d_{p}N\mathbf x_{u}(q),\mathbf x_{v}(q)\rangle +\langle (N\circ \mathbf x)(q),\mathbf x_{vu}(q)\rangle$$

och med avseende på v

$$0= \langle d_{p}N\mathbf x_{v}(q),\mathbf x_{u}(q)\rangle +\langle (N\circ \mathbf x)(q),\mathbf x_{uv}(q)\rangle$$

Eftersom $\mathbf x_{uv}=\mathbf x_{vu}$ ser vi att $\langle d_{p}N\mathbf x_{u}(q),\mathbf x_{v}(q)\rangle =\langle \mathbf x_{v}(q), d_{p}N\mathbf x_{u}(q),\rangle$.

(c)

Gausskrökningen av S i p (med avseende på N) derfinieras som $K(p)=\mbox{det}(-d_{p}N)$ medan medelkrökningen ges av $H(p)=\mbox{trace}(-d_{p}N)/2$.

(d)

Vi väljer en ON-bas $e_{1},\,e_{2}$ av egenvektorer till -d_pN hörande till egenvärdena k₁ respektive k₂. Detta är möjligt eftersom -d_pN är självadjungerad.

I denna bas representeras -d_pN av matrisen

$$\left( \begin{array} {rr} k_{1}&0\\ 0 &k_{2} \end{array}\right).$$

Den andra fundamentalformen är

$$II_{p}(v)=II_{p}(ae_{1}+be_{2})=\langle -d_{p}N(ae_{1}+be_{... ...1}+bk_{2}e_{2}, ae_{1}+be_{2}\rangle =a^{2}k_{1}+b^{2}k_{2},$$

där a och b är koefficienterna för v i basen $e_{1},\,e_{2}$. Om vi väljer v till att ha längd 1, är detta normalkrökningen av S i p i riktningen v.

Vi väljer nu a och b så att v har längd 1, dvs så att a²+b²=1 (använder att basen är en ON-bas). De riktningar som är vinkelräta mot (a,b) är $\pm (b,-a)$. Normalkrökningen i dessa två riktningar är b²k₁+a²k₂. Summan av normalkörkningarna blir alltså

$$a^{2}k_{1}+b^{2}k_{2}+b^{2}k_{1}+a^{2}k_{2}= (a^{2}+b^{2})k... ...b^{2}+a^{2})k_{2}=k_{1}+k_{2}= \mbox{trace}(-dN_{p})=2H(p).$$

2.

(a)

När $\alpha(s)$ är parametriserad med båglängd definieras krökningen av $k(s)=\vert\alpha''(s)\vert$ och normalvektorn n(s) är normeringen av $\alpha''(s),$ under förutsättning att krökningen inte är .

Sätter vi $t(s)=\alpha'(s),$ så ger derivering av $\langle t,t\rangle \equiv 1$ att $\langle t,n\rangle \equiv 0$.

Kurvans binormal definieras som $b=t\times n$. Binormalen $b=t\times n$ har längd 1 eftersom t och n är vinkelräta och har längd 1.Detta ger att $t,\,n,\,b$ är en ON-bas för $\mathbb R^{3}$ och att matrisen $A=(t\,\,n,\,\,b)$ har determinant 1. Derivering ger

$$b'=t'\times n+t\times n'=kn\times n+t\times n'=t\times n'.$$

Men n är vinkelrät mot n', eftersom $\vert n(t)\vert\equiv 1$. Eftersom n också är vinkelrät mot t är $t\times n'$ en multipel $\tau$ av n. Detta defineirar torsionen $\tau(s)$ som $\langle b',n\rangle$ och vi ser att $b'=\tau n$.

(b)

Vi har redan att t'=kn och $b'=\tau n$ det återstår att bestämma n'. Binormalen $b=t\times n$ har längd 1 eftersom t och n är vinkelräta och har längd 1. Detta ger att $n=b\times t$ och derivering ger

$$n'=b'\times t+b\times t'=\tau n\times t+k b\times n=-kt-\tau b,$$

som är den tredje av Frenets ekvationer.

Vi skriver Frenets ekvationer på matrisform:

$$A'=A \left( \begin{array} {rrr} 0&-k &0\\ k&0&\tau\\ 0 & -\tau&0 \end{array}\right)= A\Gamma$$

Observera att $\Gamma^{t}=-\Gamma$.

Antag nu att $\beta$ är en annan bådglängdsparametriserad kurva med samma krökning och torsion som $\alpha$ och låt B vara $\beta$'s motsvarighet till A. Genom att rotera rummet och kurvan $\beta$ med en rotation R kan vi förutsätta att B(0)=A(0). (Vi förutsätter att ligger i definitionsmängden för $\alpha$.)

Vi har då två lösningar A och B till ekvationen $X'=X\Gamma.$ Vi ser att C=A-B löser ekvationen och att C(0)=0. Derivering av CC^t ger $C\Gamma C^{t}+C\Gamma^{t}C^{t} =0,$ så CC^t är konstant och lika med C(0)C^t(0)=0. Detta ger att långderna av raderna i C är noll, så $C\equiv 0$. Alltså är A=B och $\beta$ och $\alpha$ har speciellt samma tangent. Därmed är $\beta-\alpha$ konstant. Genom att translatera rummet (och $\beta$) kan vi förutsätta att $\beta(0)=\alpha(0),$ och nu är $\beta=\alpha$.

Genom en rotation och en translation kan alltså $\beta$ överföras till $\alpha$.

(c)

Antag först att $\alpha$ är parametriserad med båglängd. Då är $k=\vert\alpha''\vert= \vert\alpha'\times \alpha''\vert,$ eftersom $\alpha'$ har längd 1 och är vinkelrät mot $\alpha''=kn$. Antag nu att k>0. Derivering av det sista ger $\alpha'''=k'n+k(-kt-\tau b)=-k^{2}t + k'n -k\tau b$.

Genom att subrahera lämplig multipel av första och andra raderna från den tredej i matrisen $(\alpha',\alpha'',\alpha''')$ ser vi att

$$\mbox{det}(\alpha',\alpha'',\alpha''')=\mbox{det}(t,kn,-k\tau b)=-k^{2}\tau \mbox{det}(t,n,b)=-k^{2}\tau,$$

vilket ger

$$\tau = -\frac{ \mbox{det}(\alpha',\alpha'',\alpha''')} {\vert\alpha'\times \alpha''\vert^{2}}$$

Antag nu att $\alpha$ inte är parametriserad med båglängd. Det finns då en strängt växande funktion $\phi,$ så att $\beta(s)=\alpha(\phi(s))$ är parametriserad med båglängd. Vi har $\beta'=\phi'\alpha'(\phi),$ så $\phi'=1/\vert\alpha'(\phi)\vert$.

Vi får också $\beta''=\phi''\alpha'(\phi)+(\phi')^{2}\alpha''(\phi)$ och $\beta'''=\phi'''\alpha'(\phi)+3\phi''\phi'\alpha''(\phi)+ (\phi')^{3}\alpha'''(\phi)$.

Detta ger

$$k_{\beta}=\vert\beta'\times \beta''\vert= (\phi')^{3}\vert\alpha'(\phi)\times \alpha''(\phi)\vert,$$

så

$$k_{\alpha}=\frac{\vert\alpha'\times \alpha''\vert}{\vert\alpha'\vert^{3}}.$$

Vi får också genom att dra ifrån lämpliga multipler av rader från andra att

$$\tau_{\beta}=-\frac{ \mbox{det}(\beta',\beta'',\beta''')} ... ...{(\phi')^{6}\vert\alpha'(\phi)\times \alpha''(\phi)\vert^{2}}$$

eller

$$\tau_{\alpha}= -\frac{ \mbox{det}(\alpha',\alpha'',\alpha''')} {\vert\alpha'\times \alpha''\vert^{2}} .$$

3.

(a)

Vi sätter (x,y,z)=(u(v²+1),uv,(1-u)v) och ser att v=z+y, så x=y(z+y)+u, eller u=x-y(z+y). Detta visar att $\mathbf x(u,v)=(u(v^{2}+1),uv,(1-u)v)$ är inverterbar med invers f(x,y,z)= (x-y(z+y),z+y). Vi ser att både $\mathbf x$ och dess invers är glatta. Eftersom $\mathbf x(U)=S,$ där $U=\mathbf R^{2}$ är $\mathbf x(U)$ öppen i S. För att visa att $\mathbf x$ är en lokal parametrisering och S en reguljär yta återstår det att visa att $d\mathbf x$ är injektiv. Men $(f\circ \mathbf x)(u,v)=(u,v)$ och kedjeregeln ger att $d_{p}f\circ d_{q}\mathbf x,$ där $p=\mathbf x(q),$ är identitetsfunktionen. Detta ger att $d_{q}\mathbf x$ är injektiv.

(b)

Differentialekvationen för en asymptotisk kurva $\alpha(t)=\mathbf x(u(t),v(t))$ är 0=(u')²e+2u'v'f+(v')²g. Vi bestämmer därför koefficienterna i andra fundamentalformen. Vi har

$$\begin{array} {rclcrcl} \mathbf x_{u}&=&(v^{2}+1,v,-v) & \... ...thbf x_{vv}&=&(2u,0,0)& & g&=&2uv/\sqrt{EG-F^{2}} \end{array}$$

Efter förenkling blir differentialekvationen

0=2u'v'(v²-1)+(v')²2uv=v'(2u'(v²-1)+2uvv')

som ger oss de två ekvationerna v'=0 med lösning v=konstant, respektive 2u'/u=-2vv'/(v²-1). Integration ger $-2\ln(\vert u\vert)+C=\ln\vert v^{2}-1\vert,$ där C är en godtycklig konstant. Efter exponentirering ger detta v²-1=D/u², där D är en godtycklig konstant, eller $v=\pm \sqrt{D/u^{2}+1}$

(c)

Vi ser att Gausskrökningen är K=-(1-v²)²/(EG-F²), så punkter där $v\not=\pm 1$ är hyperboliska. När v=1 är E=6, f=0 och $g=2u/\sqrt{EG-F^{2}}.$ När v=-1 är E=6, f=0 och $g= -2u/\sqrt{EG-f^{2}}$ vilket ger medelkrökningen

$$H=\pm\frac{6u}{(EG-F^{2})^{3/2}}$$

Vi ser att vi får plana paraboliska punkter när $v=\pm 1$ och $u\not=0$ och en plan punkt när (u,v)=(0,0).

I en navelpunkt är K=H² och vi ser att detta inträffar bara när u=v=0.

Ytans paraboliska punkter är alltså $(2u,\epsilon u,\epsilon (1-u)),$ där $u\not=0$ och $\epsilon=\pm 1$. De plana punkterna är $(0,\pm 1,0),$ som också är en navelpunkt.

4.

(a)

Vi har $\alpha'=(-\sin(t/\sqrt{2}),\cos(t/\sqrt{2}),0),$ så $\alpha$ är parametriserad med båglängd.

Ytans normal är $N=(1/\sqrt{x^{2}+y^{2}+z^{2}})(x,y,-z),$ så
$N(t)=(1/\sqrt{3})(\sqrt{2}\cos(t/\sqrt{2}),\sqrt{2}\sin(t/\sqrt{2}),-1).$

Vi har $\alpha''=(-\cos(t/\sqrt{2})/\sqrt{2},-\sin(t/\sqrt{2})/\sqrt{2},0).$

Den geodetiska krökningen ges av $k_{g}=\mbox{det}(\alpha',\alpha'',N),$ så

$$k_{g}=(-1/\sqrt{3}) \begin{array} {\vert rr\vert} -\sin(t/... .../\sqrt{2}&-\sin(t/\sqrt{2})/\sqrt{2} \end{array}=-1/\sqrt{6}$$

(b)

Vi har att $\alpha',\,N\times \alpha'$ är en ON-bas för T_p(S). Ett vektorfält w längs $\alpha$ kan skrivas

$$w(t)=a(t)\alpha'(t)+b(t)(N\times \alpha')(t)$$

Derivering ger

$$w'=a'\alpha'+a\alpha''+b'N\times \alpha'+bN'\times \alpha'+bN\times \alpha''$$

Eftersom w ska vara parallellt ska skalärprodukten med $\alpha'$ och $N\times \alpha'$ vara . Detta ger

$$\left\{ \begin{array} {rcl} 0&=&a'+b(N\times\alpha'')\cdot... ...lpha''\cdot(N\times\alpha'))+b'=k_{g}a+b' \end{array}\right.$$

Lösningarna till detta ekvationssystem ges av $\mbox{exp}(A^{k_{g}t})w(0)$ (använder att k_g är konstant). Men

$$\mbox{exp}(A^{k_{g}t})=\left( \begin{array} {rrr} \cos(-t/... ...)\\ -\sin(-t/\sqrt{6})&\cos(-t/\sqrt{6}) \end{array}\right)$$

som alltså är den matris som representerar paralelltransport från $\alpha(0)$ till $\alpha(t)$ i basen $\alpha',\,N\times \alpha'$.

Svaret ges av matrisen ovan med $t=2\sqrt{2}\pi$.

5.

(a)

Låt $N=f\bar{N},$ där $f=1/\vert\bar{N}\vert,$ som är en Gaussavbildning för ytan. Vi ansätter -dN_p=aw₁+cw₂ och -dN_pw₂=bw₁+dw₂, så att -dN_p representeras av matrisen

$$\left( \begin{array} {rr} a & b\\ c & d \end{array}\right)$$

i basen $w_{1},\,w_{2}$. Detta ger att medelkrökningen är (a+d)/2. För att komma åt a och d tar vi kryssprodukt med w₁ respektive w₂ och får

$$\begin{array} {rcl} -dN_{p}w_{1}\times w_{2}&=&aw_{1}\times... ... -dN_{p}w_{2}\times w_{1}&=&-dw_{1}\times w_{2}\\ \end{array}$$

Eftersom $w_{1}\times w_{2}$ är en normal till tangentrummet är $(w_{1}\times w_{2})\cdot N\not=0$. Vi får

$$H=\frac{a+d}{2}= \frac{(-dN_{p}w_{1}\times w_{2})\cdot N-(dN_{p}w_{2}\times w_{1})\cdot N} {2(w_{1}\times w_{2})\cdot N}$$

Efter omskrivning med determinanter blir detta

$$H=-\frac{\mbox{det}(N,dN_{p}w_{1}, w_{2})+\mbox{det}(N,w_{1},dN_{p}w_{2})} {2\mbox{det}(N,w_{1},w_{2})}$$

Antag att $\alpha(0)=p$ och $\alpha'(0)=w$. Vi har då att

$$\begin{array} {rcl} d_{p}Nw&=& (N\circ \alpha)'(0)=((f\cir... ...)=\\ &=& d_{p}f(w)\bar{N}(p)+f(p)d_{p}\bar{N}(w) \end{array}$$

Använder vi nu att $N=f\bar{N}$ och $dN=df\bar{N}+fd\bar{N}$ har vi att $\mbox{det}(\bar{N},d\bar{N}_{p}w_{1},w_{2})= f^{2}\mbox{det}(N,dN_{p}w_{1},w_{2})$ och att $\mbox{det}(\bar{N},w_{1},d\bar{N}_{p}w_{2})= f^{2}\mbox{det}(N,w_{1},dN_{p}w_{2})$ samt
$\mbox{det}(\bar{N},w_{1},w_{2})=f\mbox{det}(N,w_{1},w_{2})$. Detta ger oss till slut formeln

$$H=-\frac{\mbox{det}(\bar{N},d\bar{N}_{p}w_{1}, w_{2})+\mbox... ...}w_{2})} {2\vert\bar{N}\vert\mbox{det}(\bar{N},w_{1},w_{2})}$$

(b)

Gradienten till f(x,y,z)=xyz är $\bar{N}=(1/x,1/y,1/z)$. Vi har att $d\bar{N}$ i standardbasen för $\mathbb R^{3}$ representeras av Jacobis matris som i detta fall blir den diagonala matrisen med -1/x², -1/y² och -1/z² längs huvuddiagonalen.

Vi har att w₁=(x,-y,0) och w₂=(0,y,-z) är en bas för tangentrummet i $(x,y,z)\in S$. Vi ser att $d\bar{N}w_{1}=(-1/x,1/y,0)$ och $d\bar{N}w_{2}=(0,-1/y,1/z)$. Detta ger $d\bar{N}w_{1}\times w_{2}=(-z/y,-z/x,-y/x)$ och $w_{1}\times d\bar{N}w_{2}=(-y/z,-x/z,-x/y)$. Skalärprodukt med $\bar{N}$ ger nu -z/(xy)-z/(xy)-y/(zx)=-2z²-y² respektive -y/(zx)-x/(zy)-x/(yz)=-y²-2x². Vi har också $w_{1}\times w_{2}=(zy,xz,xy)$ har skalärprodukt $zy/x+xz/y+xy/z=1/x^{2}+1/y^{2}+1/z^{2}=\vert\bar{N}\vert^{2}$. Detta ge nu

$$H=\frac{x^{2}+y^{2}+z^{2}}{(1/x^{2}+1/y^{2}+1/z^{2})^{3/2}}.$$

6.

(a)

Att normalplanet tangerar enhetssfären betyder att planet skär sfären i precis en punkt och därför är tangentplan till sfären. Om skärningspunkten är p är alltså vektorn från origo till p en enhetsnormal till normalplanet, dvs $p=\epsilon t,$ där $t=\alpha'$ och $\epsilon=\pm 1$.

Eftersom p ska ligga i normalplanet ska vi ha $\epsilon t(s)=p(s)=\alpha(s)+A(s)n(s)+B(s)b(s)$. Omvänt, om detta gäller är villkoret i uppgiften uppfyllt. Derivering ger

$$\epsilon k n= t+A'n+A(-kt-\tau b)+B'b+B\tau n$$

Eftersom $t,\,n,\,b$ är en bas ger detta ekvationssystemet

$$\left\{ \begin{array} {rclcrcl} 0&=&1-kA& \mbox{~~~}& A&=&... ...on k\\ 0&=& -\tau A+B' & & B'&=&\tau/k\\ \end{array}\right.$$

Andra och tredje raderna ger $BB'= k'/k^{3}+\epsilon$ och därmed $B=\pm \sqrt{-1/k^{2}+2\epsilon s+C},$ där konstanten C ska väljas så att B blir definierad i närheten av s₀. Den andra ekvationen ger nu $\tau=\pm (k'/k^{3}+\epsilon k)(-1/k^{2}+2\epsilon s + C)^{-1/2}$. Insättning ger att dessa värden på A, B och $\tau$ löser ekvationssystemet för givet k.

Antag nu att $k:I\rightarrow \mathbb R$ är given liksom $s_{0}\in I$. Definiera A, B och $\tau$ som ovan för ett val av C, så att samtliga är definierade i närheten av s₀. Låt $\alpha$ vara en båglängsparametriserad kurva med krökning k och torsion $\tau$.

Ekvationssystemet ovan visar nu att $\alpha+An+bB-\epsilon t$ har derivata $\equiv 0$ vilket ger att $\alpha+An+bB-\epsilon t=q,$ där q är konstant. Ersätter vi $\alpha$ med kurvan $\beta=\alpha+q$ får vi en kurva med samma tangentvektor, normal, binormal, krökning och torsion, så att $\beta+An+bB=\epsilon t$. Detta visar att det givet k och s₀ finns en kurva definerad i närheten av s₀ som uppfyller villkoret i uppgiften.

(b)

Lösningen av a) visade att de möjliga värdena på torsionen är

$$\tau=\pm (k'/k^{3}+\epsilon k)(-1/k^{2}+2\epsilon s + C)^{-1/2},$$

där $\epsilon=\pm$ och C är en konstant (som måste väljas med omsorg).