- (a)
- Låt
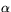 vara en glatt kurva på S, sådan att
vara en glatt kurva på S, sådan att
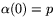 . Då är
. Då är 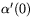 en tangentvektor till S i p.
en tangentvektor till S i p.
- (b)
- Låt
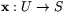 vara en lokal pramterisering av
S kring p, med
vara en lokal pramterisering av
S kring p, med 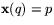 .
.En glatt kurva
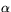 i
i 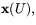 kan då skrivas
kan då skrivas
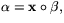 för en glatt kurva
för en glatt kurva
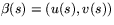 i U med
i U med 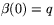 . Kedjeregeln ger att
. Kedjeregeln ger att
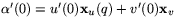 . Detta visar
att tangentvektorer till S i p är linjärkombinationer av
vektorerna
. Detta visar
att tangentvektorer till S i p är linjärkombinationer av
vektorerna 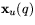 och
och 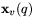 .
.Om vi väljer
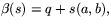 ser vi att
ser vi att 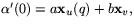 så att alla linjärkombinationer är
tangentvektorer, så Tp(S) är ett linjärt delrum till
så att alla linjärkombinationer är
tangentvektorer, så Tp(S) är ett linjärt delrum till 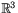 . Eftersom
. Eftersom 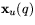 och
och 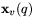 är
linjärt oberoende har tangentrummet dimension 2.
är
linjärt oberoende har tangentrummet dimension 2.
- (c)
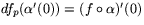 .
. - (d)
- Låt
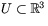 vara den öppna delmängden till
vara den öppna delmängden till
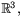 som består av hela rummet utom planen
som består av hela rummet utom planen 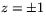 . Funktionen
. Funktionen 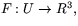
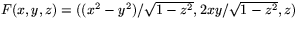 är
uppenbart glatt och restringerar till f på S. Observera att
(vi utnyttjar att x2+y2+z2=1)
är
uppenbart glatt och restringerar till f på S. Observera att
(vi utnyttjar att x2+y2+z2=1)
så att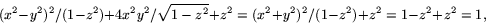
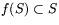 . Därmed är f glatt.
. Därmed är f glatt.
En normal till tangentrummet i p ges av (1,0,0), så
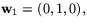
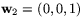 är en bas för
tangentrummet.
är en bas för
tangentrummet.
Vi har att Jacobis matris för dF ges av (
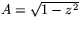 )
)
Vi har att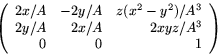
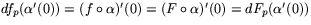 . Speciellt har vi
. Speciellt har vi
så i basen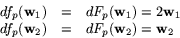
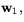
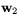 representeras dfp
av multiplikation med
representeras dfp
av multiplikation med
som har determinant 2.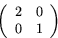
- (a)
- Tangentvektorn ges av normeringen av
så
Normalvektorn ges av normeringen av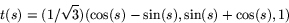
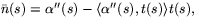 där
där
Detta ger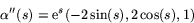
och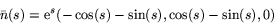
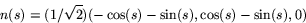
- (b)
- Krökningen ges av
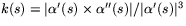 . Enligt ovan har vi
. Enligt ovan har vi
Torsionen ges av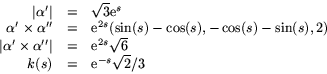
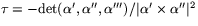 . Vi har
. Vi har
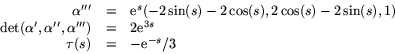
- (c)
- Mängden
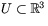 av punkter där z>0 är
öppen. Om
av punkter där z>0 är
öppen. Om 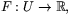
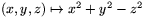 är glatt och har gradient (2x,2y,-2z), så
är ett reguljärt värde för F. Eftersom S=F-1(0), är S en
reguljär yta.
är glatt och har gradient (2x,2y,-2z), så
är ett reguljärt värde för F. Eftersom S=F-1(0), är S en
reguljär yta.
- (d)
- Vi sätter
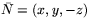 och låter Gaussavbildningen N
vara normeringen av
och låter Gaussavbildningen N
vara normeringen av 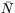 . Den geodetiska krökningen ges av
. Den geodetiska krökningen ges av
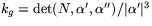 eller
eller
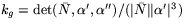 . Vi får alltså
. Vi får alltså
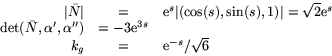
- (a)
- Derivering ger
vilket ger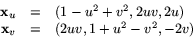
Av detta ser vi att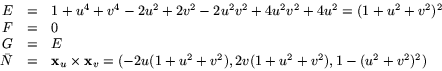
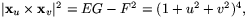 så
så 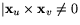 och
och 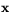 är reguljär.
är reguljär.
- (b)
- Vi har
vilket ger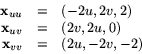
Av detta följer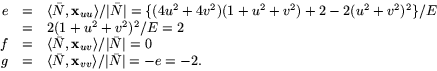
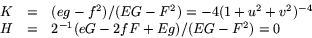
- (c)
- De asymptotiska kurvorna är av formen
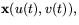 där 0=E(u')2+2Fu'v'+G(v')2=2(u'-v')(u'+v'), dvs
där 0=E(u')2+2Fu'v'+G(v')2=2(u'-v')(u'+v'), dvs 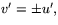 eller
eller 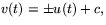 där c är en godtycklig konstant.
där c är en godtycklig konstant.
Av detta drar vi slutsaten att ![]()
![]() är den kontinuerliga funktionen
är den kontinuerliga funktionen ![]() . Av samma skäl är
. Av samma skäl är ![]() för någon
skalärvärd funktion
för någon
skalärvärd funktion ![]() .
.
Om ![]() finns det (på grund av kontinuitet) ett
finns det (på grund av kontinuitet) ett
![]() så att
så att ![]() när
när ![]() . Av detta drar vi slutsatsen att
. Av detta drar vi slutsatsen att ![]() för dessa värden på t och speciellt är N'(t0)=0, vilket
strider mot att
för dessa värden på t och speciellt är N'(t0)=0, vilket
strider mot att ![]() . Allstå är
. Allstå är ![]() och N' och
och N' och ![]() linjär beroende, dvs
linjär beroende, dvs ![]() är en egenvektor till -dN.
är en egenvektor till -dN.
Detta visar att C är en krökningslinje.
Detta är i sin tur ekvivalent med att ![]() . Derivering ger
. Derivering ger ![]() och
och ![]() , så villkoret är
ekvivalent med att x t+y b är konstant, för några konstanter x
och y.
, så villkoret är
ekvivalent med att x t+y b är konstant, för några konstanter x
och y.
Derivering av detta ger
![]()
![]()