![]()
![]()
![]()
Vi ser att vi behöver bland annat ![]() och
och ![]() :
:
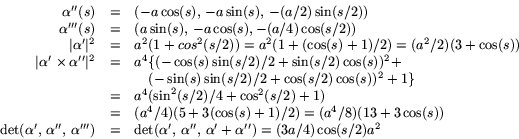
Detta ger oss nu
![]()
![]()
| t | = | |
| n | = | normeringen av |
| b | = |
Antag nu att ![]() är godtycklig. Vi kan då finna en reellvärd
funktion
är godtycklig. Vi kan då finna en reellvärd
funktion ![]() så att
så att ![]() och
och ![]() är
parametriserad med båglängd. (Man låter
är
parametriserad med båglängd. (Man låter ![]() vara omvändningen till
vara omvändningen till
![]() .) Speciellt är längden av
.) Speciellt är längden av
![]() lika med 1, så
lika med 1, så ![]() . Vi får nu
. Vi får nu
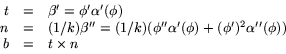
Av detta ser vi att t är normeringen av ![]() och att n ligger
i planet som spänns av
och att n ligger
i planet som spänns av ![]() och
och ![]() . Eftersom
skalären framför
. Eftersom
skalären framför ![]() är positiv pekar n åt samma sida som
är positiv pekar n åt samma sida som
![]() relativt
relativt ![]() . Detta betyder att t och n kan fås
genom att man underkastar
. Detta betyder att t och n kan fås
genom att man underkastar ![]() och
och ![]() Gram-Schmidts
ortogonaliseringsprocess.
Gram-Schmidts
ortogonaliseringsprocess.
Alternativt kan vi härleda en formel (som ger samma svar förstås). Vi
har ![]() och derivering ger
och derivering ger
![]() eller
eller
![]() . Insättning av detta
tillsammans med formeln för krökningen ger nu att tangentvektorn och
normalvektorn i punkten
. Insättning av detta
tillsammans med formeln för krökningen ger nu att tangentvektorn och
normalvektorn i punkten ![]() på
kurvan ges av
på
kurvan ges av
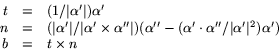
När ![]() har vi
har vi
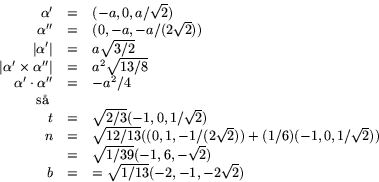
![]()
