$\parbox{5cm}{Differentialgeometri\\ V 00 \\ ~~~~\\ ~~~~}$

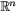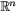
Förslag till lösning av inlämningsuppgift 2

1.

Matrismultiplikation ger

$$B^{2}=\left( \begin{array} {rrr} -1 & 0 & -c\\ 0 & -(1+c^... ...{2}) & 0 & -(1+c^{2})c\\ 0 & c(1+c^{2})& 0 \end{array}\right)$$

så om $a=\sqrt{1+c^{2}},$ så är B³=-a²B.

2.

Av B³=-aB får vi B^2k=-(-1)^ka^2k-2B² och B^2k+1=(-1)^ka^2kB, så

$$\sum_{k=0}^{\infty}f(s)^{k}B^{k}/k!=I+(\sum_{k=0}^{\infty}(-... ...}/(2k+1)!)B-(\sum_{k=1}^{\infty}(-1)^{k}a^{2k-2}f(s)^{2k})B^{2}$$

Men Taylor utvecklingarna för $\sin(x)$ och $\cos(x)$ är

$$\begin{array} {rcl} \sin(x)&=&\sum_{k=0}^{\infty}(-1)^{k}x^{... ...\ \cos(x)&=&\sum_{k=0}^{\infty}(-1)^{k}x^{2k}/(2k)!,\end{array}$$

så vi får

$$\sum_{k=0}^{\infty}f(s)^{k}B^{k}/k!=I+(\sin(af(s))/a)B+((\cos(af(s))-1)/a^{2})B^{2}$$

3.

Frenets ekvationer är i matrisformulering

$$\left( \begin{array} {ccc} t' & n' & b'\\ \end{array}\rig... ...0 & -k & 0\\ k & 0 & \tau\\ 0 & -\tau & 0 \end{array}\right)$$

Vi vet att $\tau/k=c$ är konstant, så om vi sätter

$$B=\left( \begin{array} {rrr} 0 & -1 & 0\\ 1 & 0 & c\\ 0 ... ... \begin{array} {ccc} t(s) & n(s) & b(s)\\ \end{array}\right)$$

kan ekvationerna skrivas A'(s)=A(s)k(s)B. Enligt fundamentalsaten för kurvor har detta ekvationssystem precis en lösning A(s) om vi kräver A(0)=I (Frenets treben standardbasen för $\mathbb R^{3}$ när s=0). Låt nu K(s) vara en primitiv funktion till k(s) med s=0. Vi har då

$$(\mbox{e}^{K(s)B})'=k(s)B\mbox{e}^{K(s)B}=\mbox{e}^{K(s)B}k(s)B\mbox{ och }\mbox{e}^{K(0)B}=\mbox{e}^{0B}=I$$

Vi ser att $\mbox{e}^{K(s)B}$ är en (den enda) lösningen till problemet. Den fösta kolonnen i $\mbox{e}^{K(s)B}$ är

$$\begin{array} {rcl} t(s)&=&(1,0,0)+(\sin(aK(s))/a)(0,1,0)+((... ...(aK(s))/a^{2},\sin(aK(s))/a,c(\cos(aK(s))-1)/a^{2}).\end{array}$$

4.

Villkoret för att R ska vara en rotation är att kolonnerna är av längd 1 och ömsesidigt ortogonala och att matrisen har determinant 1.

Vi prövar oss fram till den sökta rotationen genom att konstatera att om första raden är $(0\,\,-1\,\,0)$ får vi rätt x-koordinat i Rt(s). Om andra raden är $(1/a\,\,0\,\,c/a)$ stämmer även y-koordinaten. Väljer vi $(-c/a\,\,0\,\,1/a)$ som tredje rad i R får vi rätt z-koordinat. Kontroll visar att R är ortogonal.

5.

En primitiv funktion till k(s) är $K(s)=\arcsin(s)/\sqrt{2}$. Vi har också $a=\sqrt{2},$ så formeln för tangentvektorn är ($\cos(\theta)=\sqrt{1-\sin(\theta)},$ när $-\pi/2\leq\theta \leq \pi/2$)

$$t(s)=(-s/\sqrt{2},\sqrt{1-s^{2}}/\sqrt{2},1/\sqrt{2})$$

Vi bestämmer en primitiv funktion till $\sqrt{1-s^{2}}$ (kan göras på flera olika sätt) genom variabelsubstitution:

$$\begin{array} {rcl} \int\,\sqrt{1-s^{2}}\,ds&=&\{s=\sin u,\,... ...u)\cos(u)/2+u/2=\\ &=&s\sqrt{1-s^{2}}+\arcsin(s)/2.\end{array}$$

Detta tillsammans med villkoret $\alpha(0)=0$ ger nu

$$\alpha(s)=(-s^{2}/(2\sqrt{2}),s\sqrt{1-s^{2}})+\arcsin(s)/2,s/\sqrt{2}).$$