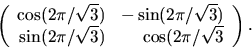Lösning till MAN500, Differentialgeometri, 99 03 20.
- 3.
- (a)
- Om
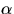 är asymptotisk gäller att
är asymptotisk gäller att 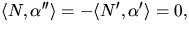 d.v.s normalkrökningen är noll. Tillsammans med
d.v.s normalkrökningen är noll. Tillsammans med 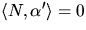 ger detta att N är
ger detta att N är 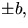 där b är kurvans
binormal.
Vi har
där b är kurvans
binormal.
Vi har 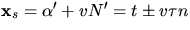 och
och 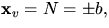 vilket ger att de är linjärt oberoende,
så regelytan är reguljär.
vilket ger att de är linjärt oberoende,
så regelytan är reguljär.
- (b)
- Observera att regelytans normal är
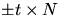 när v=0. Eftersom
när v=0. Eftersom 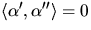 får vi
att
får vi
att  vinkelrät mot N om och endast om
vinkelrät mot N om och endast om  är
parallell med
är
parallell med 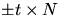 . Detta visar påståendet.
. Detta visar påståendet.
- (c)
- Vi har
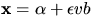 och detta ger
och detta ger 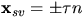 och
och 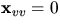 . Räkningarna ovan ger
att regelytansnormal är
. Räkningarna ovan ger
att regelytansnormal är

Detta ger g=0 och 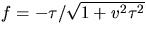 . Räkningarna
ovan ger också
. Räkningarna
ovan ger också 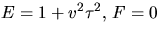 och G=1. Vi får alltså
och G=1. Vi får alltså
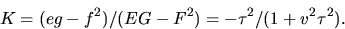
- 4.
- (a)
- Sätter vi
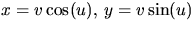 och z=u har vi att
och z=u har vi att
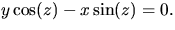 Har vi å andra sidan en lösning till denna
ekvation har vi att (y,x) är parallell med (z=u)vektorn
Har vi å andra sidan en lösning till denna
ekvation har vi att (y,x) är parallell med (z=u)vektorn
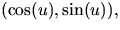 d.v.s
d.v.s 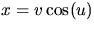 och
och 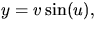 för
något
för
något 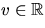 . Detta visar att S är f-1(0), där
f är den glatta funktionen
. Detta visar att S är f-1(0), där
f är den glatta funktionen 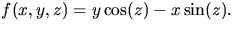 Gradienten till denna är
Gradienten till denna är
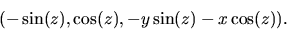
Eftersom de två första
koordinaterna inte kan vara noll samtidigt är ett reguljärt
värde och S en reguljär orienterbar yta.
- (b)
- Vi har en global parametrisering av S, så vi kan skriva
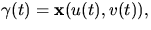 för några funktioner u(t) och
v(t). Differentialekvationen för geodeter ger att dessa
satisfierar
för några funktioner u(t) och
v(t). Differentialekvationen för geodeter ger att dessa
satisfierar
![\begin{displaymath}
\begin{array}[c]
{l}
0=u''+\Gamma_{11}^{1}(u')^{2}+2\Gamma_...
...2}+2\Gamma_{12}^{2}u'v'+
\Gamma_{22}^{2}(v')^{2}
\end{array} \end{displaymath}](img26.gif)
Vi beräknar Kristoffelsymbolerna:
![\begin{displaymath}
\begin{array}[c]
{l}
\mathbf x_{u}=(-v\sin(u),v\cos(u),1)\\...
...
(v/(1+v^{2}))\mathbf x_{u}+(1/\sqrt{1+v^{2}})N.
\end{array} \end{displaymath}](img27.gif)
Den första ekvationen i differentialekvationen ovan blir alltså

Detta ger att u'=c/(1+v2), där c är en konstant. Vi kan
förutsätta att 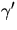 har längd ett (vi vet att den är konstant
har längd ett (vi vet att den är konstant
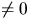 eftersom
eftersom 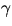 är en geodet). Vi får nu att
är en geodet). Vi får nu att
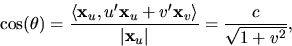
vilket visar påståendet.
- 5.
- En isometri bevarar inre begrepp, så som Gausskrökning och
geodeter och båglängd. Längs medianernerna
 är
Gausskrökningen noll och den är nollskild för övrigt. Detta ger att
en isometri f måste bevara dessa medianer eller byta plats på
dem. Eftersom meridianerna är geodeter på en rotations yta och
vinklar bevaras följer det att f måste avbilda en meridian på en
meridian ty de är de enda geodeterna som skär medianerna
är
Gausskrökningen noll och den är nollskild för övrigt. Detta ger att
en isometri f måste bevara dessa medianer eller byta plats på
dem. Eftersom meridianerna är geodeter på en rotations yta och
vinklar bevaras följer det att f måste avbilda en meridian på en
meridian ty de är de enda geodeterna som skär medianerna  vinkelrätt. Eftersom båglängd längs medianerna
vinkelrätt. Eftersom båglängd längs medianerna  bevaras
följer det att f måste vara av följande typer:
bevaras
följer det att f måste vara av följande typer:
- en rotation runt z-axeln
- en spegling i ett plan vinkelrätt mot xy-planet
- en spegling i xy-planet sammansatt med någon av de övriga
två typerna.
Att dessa ger isometrier av torusen följer av att de är isometrier
av 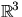 . Vi har konstaterat att en isometri av torusen är
restriktion av en isometri av
. Vi har konstaterat att en isometri av torusen är
restriktion av en isometri av 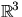 . De tillåtna
isometrierna är
. De tillåtna
isometrierna är

där 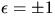 .
. - 6.
- (a)
- Vi vet att parallelltransport bevarar första
fundamentalformen, så det räcker att visa att parallelltransport
är linjär. Låt
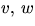 vara vektorer i
vara vektorer i 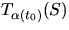 och
och
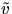 samt
samt 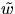 parallella vektor fält längs
parallella vektor fält längs 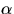 med
med 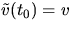 och
och 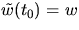 . För skalärer
. För skalärer
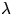 och
och 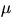 är då vektorfältet
är då vektorfältet 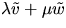 parallellt längs
parallellt längs 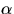 eftersom
eftersom
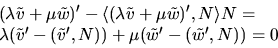
- (b)
- Sätt
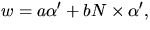 där a(t) och b(t) är
funktioner som vi ska bestämma så att w är parallellt längs
där a(t) och b(t) är
funktioner som vi ska bestämma så att w är parallellt längs
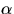 . Vi har
. Vi har

Vi har att N är vinkelrät mot 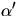 och N' så
och N' så 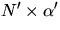 är en multipel av N. (Eftersom
är en multipel av N. (Eftersom 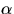 är en
krökningslinje är N' och
är en
krökningslinje är N' och 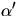 parallella, så
parallella, så 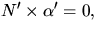 men påståendet i uppgiften
gäller utan denna förutsättning). Eftersom
men påståendet i uppgiften
gäller utan denna förutsättning). Eftersom 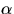 är
parametriserad med båglängd har vi att
är
parametriserad med båglängd har vi att
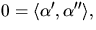 vilket också ger att
vilket också ger att 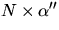 är en multipel av
är en multipel av 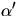 . Vi ska ha
. Vi ska ha
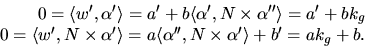
Detta ger
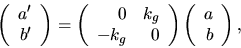
som har lösningarna 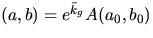 där
där
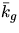 är en rimitiv funktion till kg och w(t0)
har koordinaterna (a0,b0) i den valda basen och
är en rimitiv funktion till kg och w(t0)
har koordinaterna (a0,b0) i den valda basen och
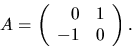
Vi ska dessutom välja 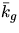 så att
så att 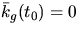 . Eftersom
. Eftersom
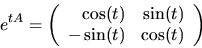
har vi w(t) har koordinaterna
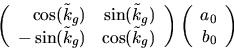
Detta visar påståendet.
- (c)
- C parametriseras av
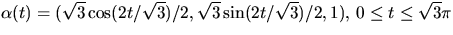 som är en parametrisering med
båglängd. Eftersom medianer på en rotationsyta är krökningslinjer
kan vi använda resultatet ovan. Vi har N(x,y,z)=(x,y,z/2)
(t.ex) och får
som är en parametrisering med
båglängd. Eftersom medianer på en rotationsyta är krökningslinjer
kan vi använda resultatet ovan. Vi har N(x,y,z)=(x,y,z/2)
(t.ex) och får
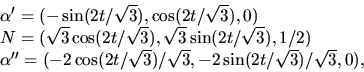
så 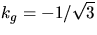 . Vi väljer
. Vi väljer 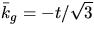 och får
att parallelltransport ett varv längs
och får
att parallelltransport ett varv längs 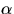 med början i
med början i
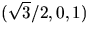 reprsenteras av
reprsenteras av
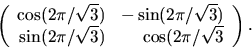
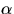 är asymptotisk gäller att
är asymptotisk gäller att 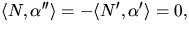 d.v.s normalkrökningen är noll. Tillsammans med
d.v.s normalkrökningen är noll. Tillsammans med 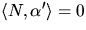 ger detta att N är
ger detta att N är 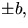 där b är kurvans
binormal.
Vi har
där b är kurvans
binormal.
Vi har 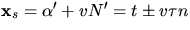 och
och 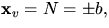 vilket ger att de är linjärt oberoende,
så regelytan är reguljär.
vilket ger att de är linjärt oberoende,
så regelytan är reguljär.
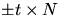 när v=0. Eftersom
när v=0. Eftersom 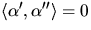 får vi
att
får vi
att  vinkelrät mot N om och endast om
vinkelrät mot N om och endast om  är
parallell med
är
parallell med 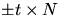 . Detta visar påståendet.
. Detta visar påståendet.
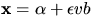 och detta ger
och detta ger 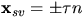 och
och 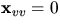 . Räkningarna ovan ger
att regelytansnormal är
. Räkningarna ovan ger
att regelytansnormal är

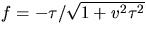 . Räkningarna
ovan ger också
. Räkningarna
ovan ger också 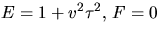 och G=1. Vi får alltså
och G=1. Vi får alltså
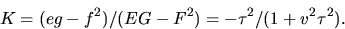
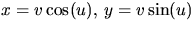 och z=u har vi att
och z=u har vi att
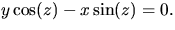 Har vi å andra sidan en lösning till denna
ekvation har vi att (y,x) är parallell med (z=u)vektorn
Har vi å andra sidan en lösning till denna
ekvation har vi att (y,x) är parallell med (z=u)vektorn
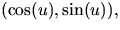 d.v.s
d.v.s 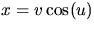 och
och 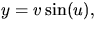 för
något
för
något 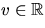 . Detta visar att S är f-1(0), där
f är den glatta funktionen
. Detta visar att S är f-1(0), där
f är den glatta funktionen 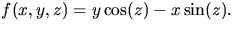 Gradienten till denna är
Gradienten till denna är
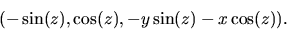
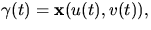 för några funktioner u(t) och
v(t). Differentialekvationen för geodeter ger att dessa
satisfierar
för några funktioner u(t) och
v(t). Differentialekvationen för geodeter ger att dessa
satisfierar
![\begin{displaymath}
\begin{array}[c]
{l}
0=u''+\Gamma_{11}^{1}(u')^{2}+2\Gamma_...
...2}+2\Gamma_{12}^{2}u'v'+
\Gamma_{22}^{2}(v')^{2}
\end{array} \end{displaymath}](img26.gif)
![\begin{displaymath}
\begin{array}[c]
{l}
\mathbf x_{u}=(-v\sin(u),v\cos(u),1)\\...
...
(v/(1+v^{2}))\mathbf x_{u}+(1/\sqrt{1+v^{2}})N.
\end{array} \end{displaymath}](img27.gif)

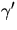 har längd ett (vi vet att den är konstant
har längd ett (vi vet att den är konstant
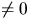 eftersom
eftersom 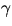 är en geodet). Vi får nu att
är en geodet). Vi får nu att
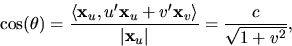

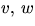 vara vektorer i
vara vektorer i 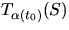 och
och
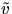 samt
samt 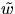 parallella vektor fält längs
parallella vektor fält längs 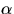 med
med 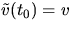 och
och 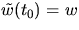 . För skalärer
. För skalärer
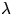 och
och 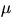 är då vektorfältet
är då vektorfältet 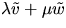 parallellt längs
parallellt längs 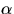 eftersom
eftersom
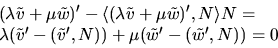
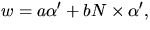 där a(t) och b(t) är
funktioner som vi ska bestämma så att w är parallellt längs
där a(t) och b(t) är
funktioner som vi ska bestämma så att w är parallellt längs
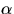 . Vi har
. Vi har

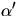 och N' så
och N' så 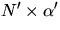 är en multipel av N. (Eftersom
är en multipel av N. (Eftersom 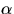 är en
krökningslinje är N' och
är en
krökningslinje är N' och 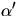 parallella, så
parallella, så 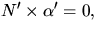 men påståendet i uppgiften
gäller utan denna förutsättning). Eftersom
men påståendet i uppgiften
gäller utan denna förutsättning). Eftersom 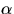 är
parametriserad med båglängd har vi att
är
parametriserad med båglängd har vi att
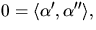 vilket också ger att
vilket också ger att 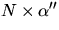 är en multipel av
är en multipel av 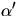 . Vi ska ha
. Vi ska ha
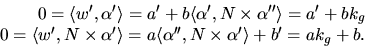
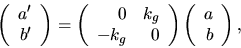
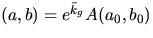 där
där
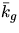 är en rimitiv funktion till kg och w(t0)
har koordinaterna (a0,b0) i den valda basen och
är en rimitiv funktion till kg och w(t0)
har koordinaterna (a0,b0) i den valda basen och
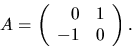
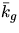 så att
så att 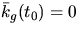 . Eftersom
. Eftersom
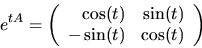
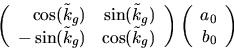
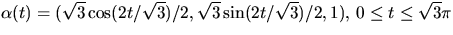 som är en parametrisering med
båglängd. Eftersom medianer på en rotationsyta är krökningslinjer
kan vi använda resultatet ovan. Vi har N(x,y,z)=(x,y,z/2)
(t.ex) och får
som är en parametrisering med
båglängd. Eftersom medianer på en rotationsyta är krökningslinjer
kan vi använda resultatet ovan. Vi har N(x,y,z)=(x,y,z/2)
(t.ex) och får
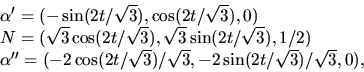
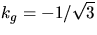 . Vi väljer
. Vi väljer 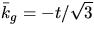 och får
att parallelltransport ett varv längs
och får
att parallelltransport ett varv längs 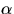 med början i
med början i
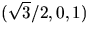 reprsenteras av
reprsenteras av