- (a)
- Vi har
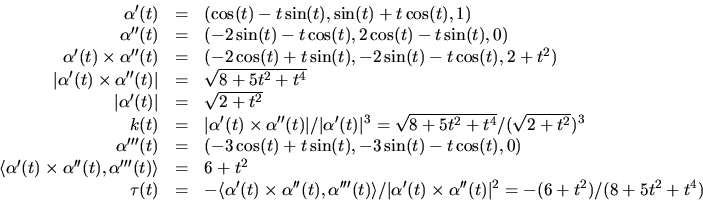
- (b)
- S är funktionsytan till
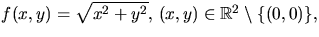 som är glatt. Därför är S en reguljär
yta.
som är glatt. Därför är S en reguljär
yta.
Eftersom
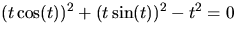 ligger spåret av
ligger spåret av
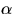 på S när t>0.
på S när t>0.
För en kurva
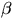 paramteriserad med båglängd ges den
geodetiska krökningen av
paramteriserad med båglängd ges den
geodetiska krökningen av 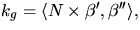 där N är en normal för ytan. Vi kan
välja
där N är en normal för ytan. Vi kan
välja 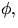 så att
så att 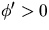 och
och 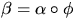 är
parametriserad med båglängd. Vi har då
är
parametriserad med båglängd. Vi har då 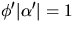 och
och
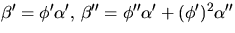 .
Detta ger, efter förenkling,
.
Detta ger, efter förenkling,
Vi väljer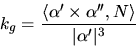
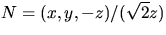 och får
och får
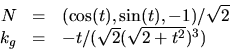
- (a)
- Vi parametriserar ytan med
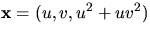 och
får
och
får
Vi får alltså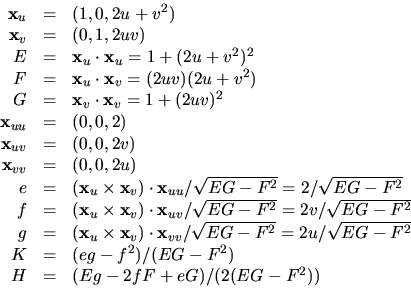
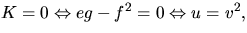 d.v.s Gausskrökningen är i punkterna
(v2,v,2v4) där
d.v.s Gausskrökningen är i punkterna
(v2,v,2v4) där 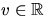 .
.
- (b)
- I en plan punkt gäller att K=H=0. Vi har
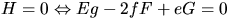 . Vi vet redan att
. Vi vet redan att 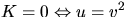 . Detta ger nu
. Detta ger nu
där w=v2. Funktonen f(w)=w3+w/+1 har derivata f'(w)=3w2+1, så f är strängt växande. Eftersom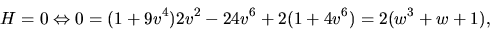
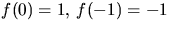 har f precis ett reellt nollställe och detta
är negativt. Men w=v2, så H saknarnollställen, när
K=0. Vi får att plana punkter saknas.
har f precis ett reellt nollställe och detta
är negativt. Men w=v2, så H saknarnollställen, när
K=0. Vi får att plana punkter saknas.
- (c)
- Differentialekavtionen för en asymptotisk kurva är i lokalframställning
e(u')2+2fu'v'+g(v')2=0.
Vi har u=-5t2/4 och v=t. Detta ger
Vilket är sant. Kurvan är alltså asymptotisk.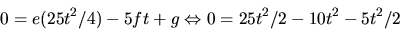
- (a)
- Vi väljer en lokal parametrisering
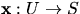 kring
kring 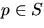 . Då är
. Då är 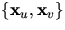 en bas för
Tp(S). Det räcker därför att visa att
en bas för
Tp(S). Det räcker därför att visa att 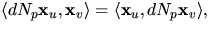 eller, med bekvämare beteckningar, att
eller, med bekvämare beteckningar, att 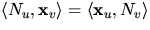 . Men derivering av
. Men derivering av 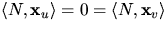 med
avseende på v respektive v ger
med
avseende på v respektive v ger
och därmed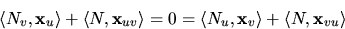
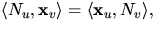 eftersom
eftersom 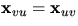 .
. - (b)
- Eftersom
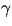 är en geodet är den (så när som på en
konstant
är en geodet är den (så när som på en
konstant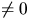 ) parametriserad med båglängd och
) parametriserad med båglängd och 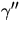 är en
multipel av så väl ytans normal som kurvans normal. Detta ger att
t och b ligger i tangentrummet. De bildar en bas för detta
eftersom de är ortogonala och rummet har dimension 2.
är en
multipel av så väl ytans normal som kurvans normal. Detta ger att
t och b ligger i tangentrummet. De bildar en bas för detta
eftersom de är ortogonala och rummet har dimension 2.
- (c)
- Eftersom
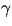 är en geodet har vi
är en geodet har vi 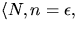 där
där 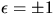 . Detta ger
. Detta ger
I ON-basen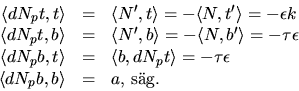
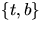 är matrisen för dNp därför
är matrisen för dNp därför
Eftersom K=0 är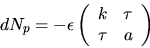
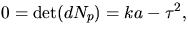 så
så
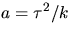 . Eftersom
. Eftersom 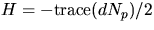 får vi alltså
får vi alltså
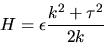
- (a)
- Eftersom ytan är reguljär kan vi välja en lokal
parametrisering
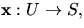 med
med 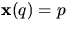 . Genom att sätta ihop
. Genom att sätta ihop 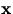 med en translation av
med en translation av
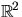 kan vi förutsätta att q=(0,0). Vi kan
parametrisera om kurvan
kan vi förutsätta att q=(0,0). Vi kan
parametrisera om kurvan 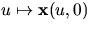 med båglängd
genom att sätta samman med en glatt funkton
med båglängd
genom att sätta samman med en glatt funkton 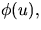 där
där
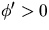 och
och 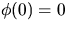 (
(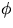 är båglängden mätt från
u=0). Detta ger att
är båglängden mätt från
u=0). Detta ger att 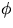 är inverterbar och funktionen
är inverterbar och funktionen
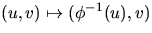 är en diffemorfi från U till sin
bild V, säg, med invers
är en diffemorfi från U till sin
bild V, säg, med invers 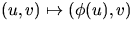 . Sätter vi
samman
. Sätter vi
samman 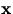 med denna får vi en lokal paramterisering, igen
kallad
med denna får vi en lokal paramterisering, igen
kallad 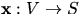 av S
kring p, som uppfyller villkoren.
av S
kring p, som uppfyller villkoren.
- (b)
- Eftersom vi startade med en godtycklig paramtrisering i (a) kan vi anta att den vara en parametrisering vars koordinatkurvor är krökningslinjer. Den omparametrisering vi gjorde i (a) förändrar inte det faktum att koordinatkurvorna är krökningslinjer. Eftersom K=0 är principalkrökningen i en av koordinatkurvornas riktning. Vi kan lika gärna förutsätta att detta inträffar när v är konstant. Detta betyder att dessa kurvor är asymptotiska.
- (c)
- Vi vet nu att vi kan välja en lokal parametrisering
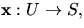 med
med 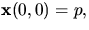
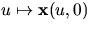 parametriserad med båglängd och koordinatkurvorna
u=konstant krökningslinjer och v=konstant såväl
krökningslinjer som asymptotiska kurvor. För att visa att dessa är
räta linjer räcker det att visa att
parametriserad med båglängd och koordinatkurvorna
u=konstant krökningslinjer och v=konstant såväl
krökningslinjer som asymptotiska kurvor. För att visa att dessa är
räta linjer räcker det att visa att 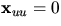 .
.Eftersom v=konstant ger en asymptotisk koordinatkurva har vi
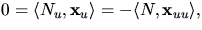 så
så
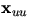 ligger i tangentrummet.
ligger i tangentrummet.
Eftersom koordinatkurvorna u=konstant är krökningslinjer har vi
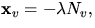 där
där
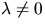 eftersom p inte är en navelpunkt (
eftersom p inte är en navelpunkt (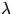 är
den nollskilda prinicpalkrökningen). Eftersom koordinatkurvorna
v=konstant är asymptotiska har vi Nu=0
är
den nollskilda prinicpalkrökningen). Eftersom koordinatkurvorna
v=konstant är asymptotiska har vi Nu=0
Eftersom prinicpalriktningar är ortogonala när principalkrökningarna är olika, har vi att
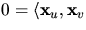 . Vi får nu
. Vi får nu
Detta ger att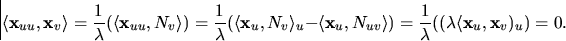
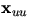 är en multipel av
är en multipel av 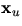 .
.Vi får också
Eftersom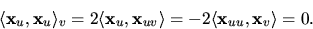
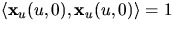 ger detta nu
ger detta nu 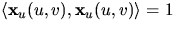 .
.Derivering av denna likhet ger
och där med är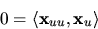
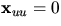 och koordinatkurvorna
v=konstant räta linjer.
och koordinatkurvorna
v=konstant räta linjer.