- (a)
- Vad menas med en parametriserad geodet
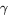 på en reguljär
yta S?
på en reguljär
yta S?
- (b)
- Härled differentialekvationerna för parametriserade geodeter på S i en lokal parametrisering.
- (a)
- Vad menas med en reguljär yta?
- (b)
- Visa att en sådan yta har en grafparametrisering kring varje punkt.
- (a)
- Visa att
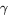 har krökning
har krökning 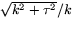 och
torsion
och
torsion
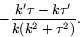
- (b)
- Visa att spåret av
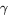 ligger på en cirkel om och endast om
ligger på en cirkel om och endast om
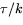 är konstant.
är konstant.
- (a)
- Visa att f(x,y,z)=(z4-z2+1)-1/2(x2-y2,2xy,z)
definierar en glatt funktion
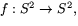 där
där
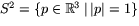 .
. - (b)
- Finns det några
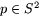 sådana att dfp är en isometri? Vilka
i så fall?
sådana att dfp är en isometri? Vilka
i så fall?
- (a)
- Visa att mängden
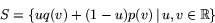
är en reguljär orienterbar yta.
- (b)
- Karaktärisera punkterna på S (elliptiska, hyperboliska,
paraboliska, plana punkter, navelpunkter).
- (c)
- Bestäm de asymptotiska kurvorna på S.
- (a)
- Bestäm alla evolutor till
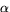 .
.
- (b)
- Ange ett villkor på
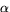 sådant att alla dess evolutor är
reguljära.
sådant att alla dess evolutor är
reguljära.
- (c)
- Visa att det finns högst en plan reguljär evoluta till
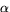 .
.