Funktionsfiler

I studio 1 beräknade vi derivatan $f'(x)$ numeriskt för olika funktioner $f(x)$. Men trots att vi använde samma formel,

$$f'(x) = \frac{f(x+h)-f(x)}{h},$$

för detta, så såg implementeringen av denna formel olika ut beroende på vad $f(x)$ var.

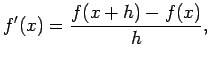Det går att göra detta mycket smidigare genom att använda s.k. funktionsfiler. En funktionsfil är som en fabrik, den tar in en råvara, t.ex. talet $x$, och returnerar en färdig produkt, t.ex. talet $x^2+1$. Vi illustrerar m.h.a.

function y = fkn(x)
y=x^2+1;

Denna funktion heter fkn och tar in talet $x$ och ger ut (returnerar) talet $y=x^2+1$. Observera ordet function som indikerar att denna m-fil är en funktionsfil. Spara denna fil under namnet fkn.m. Vi kan nu anropa denna funktion från Matlabprompten eller innifrån en vanlig skriptfil genom att skriva t.ex.

>> fkn(1.0)

vilket ger resultatet $2.0$. Detta är ju rimligt eftersom vi ger funktionen värdet $x=1.0$.

Antag nu att vill beräkna derivatan $y=f'(x)$ av $f(x)=x^2+1$ i punkten $x=2.0$ och med $h=0.001$. Vi kan göra detta genom att anropa funktionen fkn två gånger enligt nedan

>> h=0.001;
>> x=2.0;
>> y=(fkn(x+h)-fkn(x))/h

Observera likheten med formeln $f'(x) = (f(x+h)-f(x))/h$. Om vi sedan vill räkna ut derivatan av en annan funktion $f(x)$ i $x=2$ är det nu bara att ändra variabeln y i filen fkn.m.

Övning: Skriv en funktionsfil för funktionen $f(x)=x^3-x^2-x$ och räkna ut derivatan $f'(x)$ i punkterna $x=-1,-1/2,0,1/2,1$.

Övning: Räkna ut derivatan $f'(x)$ för funktionen i förra övningen i $100$ jämnt fördelade punkter i intervallet $0< x < 1$ och rita derivatan.

Tips: använd dig av funktionsfilen från övningen innan och en for-loop, enligt

h=0.001;
x=0:0.01:1; % x-values
y=x; % init vector y to store results
for i = 1:length(x) % loop through x-vector
  y(i)= % write derivative calculation here
end
plot(x,y)