Newtons metod

Det är enkelt att förstå hur Newtons metod fungerar för den skalära ekvationen f(x) = 0. Det är inte alls lika lätt att få någon känsla för ett system av ekvationer. Denna sida utgör ett försök att grafiskt illustrera fallet med två ekvationer, f(x, y) = 0 och g(x, y) = 0, i de två variablerna x och y.

Låt oss börja med att studera systemet av ekvationer på några olika sätt. För att göra resonemanget mera konkret antar vi att f(x, y) = x² - y² -  2 och g(x, y) = xy - 2. Man kan visa att de reella rötterna är ungefär x = 1.8 och y = 1.1 samt x = -1.8 och y = -1.1. Eftersom f(-x, -y) = f(x, y) (analogt för g) kommer vi enbart att studera problemet i första kvadranten av (x, y)-planet.

Några tolkningar av systemet:
 

1. f(x, y) = 0 definierar en kurva i (x, y)-planet (y = sqrt(x² - 2) i exemplet). Detta gör även g(x, y) = 0 (kurvan är y = 2 / x i exemplet). Skärningarna mellan dessa kurvor ger oss rötterna till systemet.
    
2. Vi kan betrakta (x, y, f(x, y)) som en yta i tre dimensioner, dvs. z = f(x, y) definieras som den tredje koordinaten. På motsvarande sätt definierar z = g(x, y) en funktionsyta. Skärningen mellan dessa två ytor är kurvor. Nollställena ges av de punkter där kurvorna skär (x, y)-planet.
    
3. Nästan som i 2). z = f(x, y) och  z = g(x, y) definierar funktionsytor. Skärningen mellan dessa två ytor och ytan z = 0 (dvs. (x, y)-planet) ger lösningarna.
   

Vilket synsätt man väljer är en smaksak och det kan kanske löna sig att växla synsätt.

Taylors formel

När vi härleder Newtons metod utnyttjar vi Taylorutveckling av en funktion av två variabler. Låt oss utveckla f(x, y) kring punkten (a, b):

f(a + h, b+ k) = f(a, b) + f_x(a, b) h + f_y(a, b) k + ...

där f_x och f_y får beteckna de partiella derivatorna. Låt oss fixera punkten (a, b) och definiera funktionen t(h, k) som alltså beror av h och k (som alltså får variera), genom:

t(h, k) = f(a, b) + f_x(a, b) h + f_y(a, b) k

Tripplarna (h, k, t(h, k)) definierar en yta i tre dimensioner (x svarar mot h, y mot k och z mot t(h, k)). Ytan är i själva verket tangentplanet till till funktionsytan, som ges av f(x, y), i punkten (x, y) = (a, b).

(h, k) anger hur mycket vi avlägsnar oss från (a, b). Till exempel är ju t(0, 0) = f(a, b). Om Du är en van ß-läsare så kanske Du inte tycker att det stämmer med formeln på sid. 214 (eller vad det nu kan vara i Din upplaga av tabellsamlingen). Där står att tangentplanet har framställningen:

z - f(a, b) = f_x(a, b) (x - a) + f_y(a, b) (y - b)

Eftersom h är avvikelsen från x = a, dvs. h svarar mot x - a i denna formel (analogt för k) så ser vi att det är samma uttryck.

Newtons metod

Vi står i punkten(x_j, y_j) och söker korrektioner h och k så att f(x_j + h, y_j + k) = 0 och g(x_j + h, y_j + k) = 0. Nu kan vi inte lösa detta problem direkt (det är ju lika svårt som ursprungsproblemet). Istället löser vi det linjäriserade problemet. Dvs. vi approximerar f, i en omgivning av punkten (x_j,  y_j), med tangentplanet t_f(h, k). Vi approximerar analogt g  med tangentplanet t_g(h, k) (jag har satt på _f och _g för att kunna skilja planen åt). Så:

t_f(h, k) = f(x_j,  y_j) + f_x(x_j,  y_j) h + f_y(x_j,  y_j) k,    t_g(h, k) = g(x_j,  y_j) + g_x(x_j,  y_j) h + g_y(x_j,  y_j) k

Vi kan nu relativt enkelt lösa det linjära systemet: t_f(h, k) = 0 och t_g(h, k) = 0 som ger oss approximativa korrektioner h och k. Koefficientmatrisen blir alltså Jacobianen och högerledet är -[f(x_j,  y_j), g(x_j,  y_j)]^T. Du kan nu tillämpa resonemanget ovan (de tre punkterna) på detta linjära problem. Så (om vi bortser från urartningsfall):

1. t_f(h, k) = 0 definierar en rät linje i (x, y)-planet. Detta gör även t_g(x, y) = 0. Skärningen mellan dessa linjer ger oss roten till det linjära systemet.
    
2. t_f(h, k) och t_g(h, k) definierar två tangentplan. Skärningen mellan dessa två plan är en rät linje. Roten ges av den punkt där den räta linjen skär (x, y)-planet.
    
3. Nästan som i 2). t_f(h, k) och t_g(h, k) definierar två tangentplan. Skärningen mellan dessa två plan och planet z = 0 (dvs. (x, y)-planet) ger lösningen.
   

I följande bildsvit har jag försökt att illustrera ovanstående med hjälp av grafik.

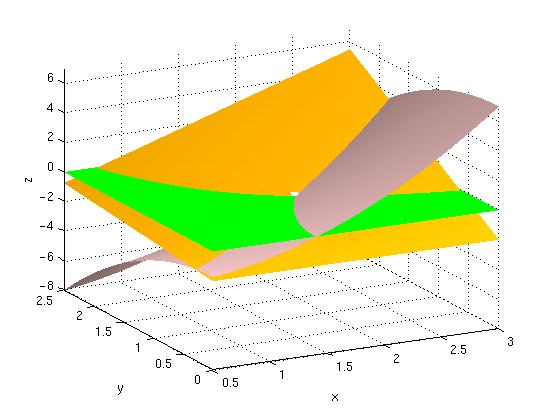
Den första bilden visar en del av funktionsytorna (f i rosaaktigt och g i gult). Den gröna ytan är en del av planet z = 0 (dvs. en del av x-y-planet). Roten är markerad med en vit fläck. Tänk igenom de tre olika synsätten när Du studerar figuren!

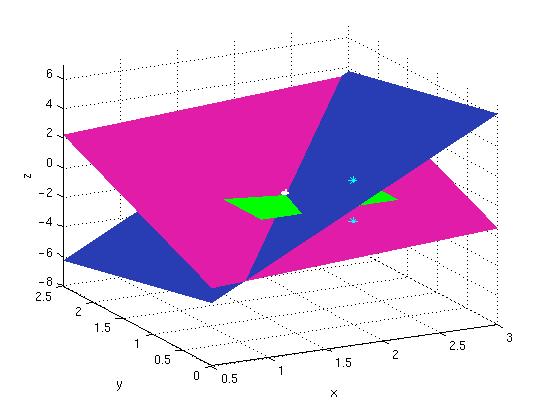
I följande bild har jag dessutom ritat ut delar av tangentplanen. Tangeringspunkterna (x_j, y_j, f(x_j, y_j)) respektive (x_j, y_j, g(x_j, y_j)) är markerade med cyanfärgade *. Planen är rödlila respektive mörkblå. Den vita fläcken är nu den approximativa lösningen.

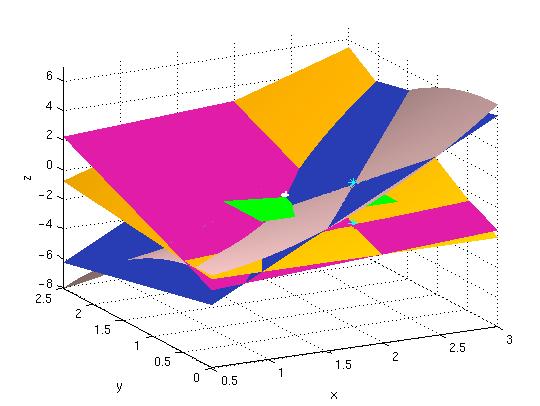
I nästa bild har jag tagit den föregående och avlägsnat funktionsytorna, för att få lite färre detaljer.