Vad är en positivt definit matris egentligen?
En positivt definit matris , A, är en kvadratisk matris som uppfyller villkoret att: xTAx > 0 för alla x där åtminstone något xk inte är noll. Om x består av idel nollor så blir givetvis xTAx = 0. Flertalet numeriker kräver dessutom att A skall vara symmetrisk. Det finns dock några få tillämpningar där A är osymmetrisk men uppfyller xTAx > 0. I kursen, liksom på denna sida, kräver vi dock symmetri; den är underförstådd.
För att bättre förstå vad en positivt definit matris är, kommer här en lista på några (men långt i från alla) egenskaper. Jag tror att enda sättet att få någon känsla för detta begrepp är att studera det ur olika synvinklar.
En positivt definit matris är positiv i någon mening. Detta är speciellt tydligt om A är en 1x1-matris, en skalär. Ty om A och x är skalära så kräver vi att Ax2 > 0 när x inte är noll. A måste alltså vara ett positivt tal.
Nästa enkla fall är när A är diagonal. Låt oss ta x = ek, kolonn k i enhetsmatrisen I. A ek är kolonn nummer k i A och ekT Aek = ak,k, så att matrisen måste ha positiva diagonalelement. Vi inser att detta även gäller om matrisen inte är en diagonalmatris, men det är då endast ett nödvändigt villkor och inte ett tillräckligt villkor.
Om inte A är diagonal så måste i alla fall diagonalen innehålla stora element. I en övning i kompendiet visas det att:
|aj,k| < [aj,j + ak,k] / 2
dvs. medelvärdet av två diagonalelement är alltid större än "motsvarande" ickediagonala element. Detta medför också att det största elementet finns på diagonalen. Observera dock att matrisens minsta element (till beloppet) kan finnas på diagonalen. Vi kommer senare att bevisa följande: om A är en 2x2-matris där a1,1 > 0 så är matrisen positivt definit om a1,1 a2,2 > a1,22. Detta innebär att vi kan göra a1,1 godtyckligt litet (> 0) förutsatt att vi kompenserar med ett stort a2,2.
Om vi har en större matris, så är det svårt att direkt se om matrisen är positivt definit eller inte. Normalt krävs mer eller mindre omfattande beräkningar. Ett relativt billigt sätt att avgöra hur det står till är att försöka beräkna matrisens Choleskyfaktorisering. Om den existerar så är matrisen positivt definit, annars inte. Så här ser det ut i Matlab för några små exempel:
>> A = [1 2; 2 3]
A =
1 2
2 3
>> chol(A)
??? Error using ==> chol
Matrix must be positive definite.
>> A = [1 2; 2 4]
A =
1 2
2 4
>> chol(A)
??? Error using ==> chol
Matrix must be positive definite.
>> A = [1 2; 2 5]
A =
1 2
2 5
>> chol(A)
ans =
1 2
0 1
Vi ser från exemplet att positiva diagonalement är ett nödvändigt villkor för att A skall vara positivt definit, men det är inte ett tillräckligt villkor.
Från föreläsningen vet vi ju att Choleskyfaktoriseringen är en variant av LDLT-faktoriseringen. Om A är positivt definit så kan man visa (övning i kompendiet) att diagonalen i D enbart innehåller positiva element, varför man kan dra roten ur dem och dividera med rötterna. Detta går inte om A inte är positivt definit (algoritmen i Matlab skiljer sig från denna handräkningsmetod, med även Matlab måste beräkna kvadratrötter).
En dyrare metod är att beräkna matrisens egenvärden. En positivt definit matris har positiva egenvärden. Det är enkelt att visa åt ena hållet. Vi vet att en symmetrisk matris har reella egenvärden. Låt oss beteckna dessa med µk (jag har inget lambda i HTML, men det jobbas på MathML) och låt motsvarande egenvektorer vara xk. En egenvektor är skild från nollvektorn, så vi får med andra ord:
A xk = µk xk => xkT A xk = µk xkT xk <=> xkT A xk = µk || xk ||22
Eftersom matrisen är positivt definit och egenvektorn har positiv längd så måste tydligen egenvärdena vara positiva. Man kan visa att omvändningen också gäller, dvs. en reell symmetrisk matris med positiva egenvärden är positivt definit.
Vi kan nu förstå villkoret i 2x2-fallet. a1,1 a2,2 - a1,22 är det(A) vilket är produkten av matrisens egenvärden (det(A) = µ1µ2 ... µn gäller för allmänna kvadratiska matriser). Denna produkt måste vara positiv. a1,1 > 0 medför att åtminstone ett egenvärde är positivt och det(A) > 0 medför att även det andra är det.
Att a1,1 > 0 medför att åtminstone ett egenvärde är positivt kan man motivera t.ex. med följande viktiga olikhet (som jag inte kommer att bevisa). Antag att A är en symmetrisk matris av ordning n med egenvärden µ1 <= µ2 <= ... <= µn. Då är den så kallade Rayleighkvoten xTAx / xTx (x är en godtycklig vektor skild från nollvektorn) begränsad av största och minsta egenvärdet dvs.
µ1 <= xTAx / xTx <= µn för alla x (inte noll).
Tag x = e1, då ger olikheten att a1,1 <= µ2 i vårt 2x2-exempel, och eftersom vi antog att a1,1 > 0 så måste ett egenvärde vara positivt.
Man kan givetvis visa när A är positivt definit direkt från definitionen. Får att slippa skriva så mycket låter vi matrisen ha elementen:
| [ a | c ] | |
| [ c | b ] |
Låter vi dessutom x ha komponenterna x och y (för att slippa index) så blir xTAx = ax2 + 2c xy + by2. Vi antar att a > 0 och kvadratkompletterar. Vi får då: ax2 + 2cxy + by2 = (sqrt(a) x + c y / sqrt(a))2 + (b - c2 / a) y2. För att detta skall vara positivt om x och y inte båda är noll får vi tydligen kräva att b - c2 / a > 0 eller (eftersom a > 0) att a b - c2 > 0.
Vi visade ovan att om A är positivt definit så är diagonalelementen positiva. I själva verket är varje så kallad principal delmatris positivt definit. En delmatris får man om man plockar ut alla element som finns på en uppsättning rader och kolonner och bildar en ny matris med dessa element (t.ex. alla element som finns i första, tredje och sjunde raden och som samtidigt ligger i femte och åttonde kolonnerna). Det är en principal delmatris om vi plockar ut samma rader och kolonner. Här följer ett Matlabexempel:
>> A
A =
211 173 139 154 168
173 221 163 134 154
139 163 241 163 139
154 134 163 221 173
168 154 139 173 211
>> p = [1 3 4] % Välj rader och kolonner
p =
1 3 4
>> S = A(p, p) % Principal delmatris
S =
211 139 154
139 241 163
154 163 221
I exemplet väljer vi ut alla element som finns i raderna och kolonnerna 1, 3 och 4. Jag har markerat dessa element med fetstil. Ett diagonalelement är ett specialfall av en principal delmatris. Man kan visa att varje principal delmatris, S, av en positivt definit matris är positivt definit. Låt oss visa beviset för ovanstående specialfall. Eftersom A är positivt definit så måste gälla att xTAx > 0 om x = [x1, 0, x3, x4, 0, 0]T om inte alla x1, x3, x4 är noll (observera att vi har valt ut element med samma index som i indexvektorn p). Man kan nu visa (gör det!) att xTAx = cTSc om c får beteckna den komprimerade vektorn c = [x1, x3, x4]T.
Vi kan ta detta ett steg till. En ledande principal delmatris är
en delmatris där man plockar ut de k första raderna och kolonnerna
(A(1:k, 1:k) med Matlabsyntax). Man kan visa att en matris är
positivt definit om den är symmetrisk och det(A(1:k, 1:k)) > 0, k
= 1, ..., n. Detta ger oss ytterligare ett bevis för specialfallet n
= 2, ty det(A(1:1, 1:1)) = a1,1 och det(A(1:2, 1:2)) =
a1,1 a2,2 - a1,22 .
Här är några sätt att skapa positivt definita matriser.
Tag en godtycklig reell matris , V, med linjärt oberoende kolonner. Då är VTV positivt definit (övning i kompendiet).
Om A är symmetrisk, men i övrigt godtycklig så kommer A + ß I att vara positivt definit om vi väljer ß tillräckligt stor (större än det mest negativa egenvärdet). Varför? Jo, om A har egenvärdena µk så har A + ß I egenvärdena µk + ß (övning, visa detta). Om vi väljer ß så att alla µk + ß > 0 (för alla k) så blir matrisen positivt definit.
Man kan också bevisa (svårare, så jag tar inte upp något bevis) att A är positivt definit om As diagonal är tillräckligt stor i följande mening (för varje diagonalelement skall gälla att det är större än summan av beloppen av de andra elementen på raden):
ak,k > | ak,1 | + | ak,2 | + ... + | ak,k-1 | + | ak,k+1 | + ... + | ak,n | för alla k
Det är enkelt att se att om A och B är positivt definita så är även A + B det. Om A är positivt definit och om V har linjärt oberoende kolonner så är även VTAV positivt definit.
En positivt definit matris är inverterbar och även inversen är positivt definit (övning i kompendiet).
Funktionstolkning
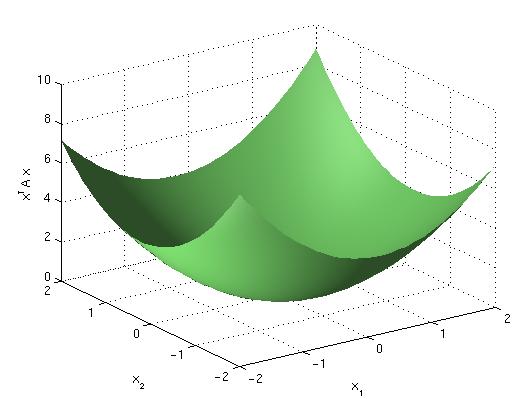
Vi kan betrakta xTAx som en funktion från Rn till R. Man brukar reda ut specialfallet n = 2 i linjäralgebrakursen. Om n = 1 så är xTAx en andragradsfunktion. Tecknet (på skalären) A anger då huruvida funktionen växer eller avtar för stora x. Då n = 2 och matrisen är positivt definit ser funktionen ut som en "kopp". Här följer en bild av xTAx (för en begränsad del av x1-x2-planet):

Egenvärden och basbyte till egenvektorsbasen visar sig vara mycket användbart för att klassificera andragradsytor av olika typ, men jag hänvisar till boken i linjär algebra för detaljer. Vi kan dock använda Rayleighkvoten för att observera följande. Antag att A är positivt definit:
µ1 <= xTAx / xTx <= µn medför att µ1 xTx <= xTAx <= µn xTx
Detta innebär att xTAx kan stängas in mellan två funktionsytor, den undre begränsningen tillväxer som µ1 xTx och den övre som µn xTx. Så, xTAx uppför sig storleksordningsmässigt ungefär som xTx. Funktionen kan växa olika snabbt i olika riktningar (det hänger på egenvärdena). Detta är enkelt att se om A är diagonal, A = diag(µ1, µ2) säg. Då är xTAx = µ1 x12 + µ2 x22. Om µ1 < µ2 tillväxer funktion snabbast i x2-riktningen och långsammast i x1-riktningen.
Omvänt kan vi se att om B är en godtycklig symmetrisk matris för vilken gäller att xTBx >= µ xTx för något positivt µ och för alla x så är B positivt definit (villkoret medför ju att xTBx > 0 om x inte är nollvektorn). Så en positivt definit matris ger alltså upphov till en växande funktion i denna mening (något som växer som xTx).
Hessianen och villkor för minimum
Vi visade på föreläsningen att en funktion av två variabler, f(x, y), har ett strikt lokalt minimum i en punkt, (a, b), om gradienten är noll i punkten och Hessianmatrisen är positivt definit. Det skall alltså gälla att fx(a, b) = fy(a, b) = 0 (jag sätter inte ut prim för att markera derivatorna) samt att H(a, b) är positivt definit där H(a, b) definieras genom:
| [ fxx(a, b) | fxy(a, b) ] | |
| [ fyx(a, b) | fyy(a, b) ] |
I detta speciella fall (n = 2) är H(a, b) positivt definit om fxx(a, b) > 0 och fxx(a, b) fyy(a, b) > (fxy(a, b))2 (vi bevisade ju detta kriterium tidigare på denna sida). Detta är den sats som finns i BETA sid. 219 (i min upplaga).
Om vi applicerar ovanstående på xTAx ser vi att x = 0 ger minimum. Gradienten blir 2 Ax och Hessianen blir 2 A.