|
Datorstudioövning 1 - 2: Assemblera hus
På dagens datorstudioövning är uppgiften att med din egen assemblerare
från DTA beräkna matriser och vektorer för "husproblemet", samt jämföra med
resultaten du beräknat
för hand enligt betinget.
Detta är en
god kontroll, dels av att du förstår tekniken med
assemblering, dels av att dina rutiner fungerar som de skall innan
vi går vidare.
Vi skall inte rita och triangulera "huset" i pdetool,
utan istället för hand skapa matriserna
p (point matrix),
t (triangle matrix), och
e (edge matrix). De två första matriserna har du nog
en viss känsla för hur de är konstruerade, medan den tredje kanske
inte är lika bekant. Så att du får göra detta för hand är både avsett
som en repetition av datastrukturerna i
p och t, samt att lära dig
lite mer om e.
Vi börjar med p: denna matris har storleken 2 x nnodes
(där nnodes betecknar antalet noder
i trianguleringen). Kolonn j
innehåller x- och y-koordinaterna
(i rad 1 respektive rad 2)
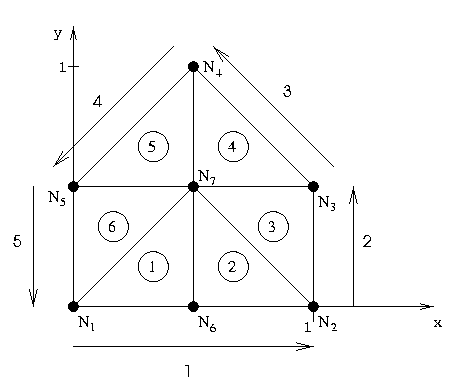
för nod nummer j i trianguleringen. Enligt figuren ovan har
vi sju stycken noder, och om vi
(som i figuren)
väljer att lägga origo i husets
nedre vänstra hörn kan vi skapa p enligt:
>> p = zeros(2, 7); % initiera p
>> p(:, 1) = [0; 0] % nod 1: x = 0; y = 0
>> p(:, 2) = [1; 0] % nod 2: x = 1; y = 0
Mata nu själv in data för övriga fem noder i p.
Vi fortsätter med t:
denna matris har storleken 4 x ntri
(där ntri betecknar antalet trianglar
i trianguleringen). Raderna 1-3 i kolonn j
innehåller nodnumren för de tre hörnen i
triangel nummer j, genomlöpta
i moturs följd. (Däremot spelar det inte någon roll
vilket av hörnen som kommer "först", d.v.s., i rad 1.)
Rad 4 anger i vilket delområde triangeln
ligger. I detta exempel tänker vi oss att vi endast har ett
delområde, hela Omega, vilket har delområdesnummer
1. Notera att området utanför Omega per
definition antas ha delområdesnummer 0.
(Kommentar: Som exempel på ett fall med flera
delområden kan vi tänka oss att "övervåningen", d.v.s.
trianglarna 4 och 5, utgör ett delområde
(nr. 1, säg),
och "nedervåningen", d.v.s. trianglarna 1, 2,
3, och 6, utgör ett annat delområde (nr. 2).
Vi skulle
då på ett enkelt sätt kunna definiera olika uttryck för t.ex.
värmekällan f beroende på om en given triangel hör
till delområde 1 eller 2.)
Enligt figuren ovan har
vi sex stycken trianglar, och vi kan skapa t enligt:
>> t = zeros(4, 6); % initiera t
>> t(:, 1) = [1; 6; 7; 1] % triangel 1; hörnnoder: 1, 6, 7;
% delområdesnummer: 1
>> t(:, 2) = [6; 2; 7; 1] % triangel 2; hörnnoder: 2, 6, 7;
% delområdesnummer: 1
Mata nu själv in data för övriga fyra trianglar i t.
Vi skapar slutligen e:
denna matris har storleken 7 x nedges. Här betecknar
nedges antalet triangelsidor som ligger på ett randsegment.
Randsegment är kurvor som skiljer två delområden åt. I vårt fall
har vi endast ett (inre) delområde, hela Omega, och
(unionen av)
randsegmenten sammanfaller därför med randen till Omega
(som skiljer Omega, delområde 1,
från området utanför Omega, "delområde" 0).
(Kommentar: Om vi istället, enligt kommentaren ovan,
tänker oss att "övervåningen" och "nedervåningen" utgör två
olika delområden skulle vi få ett extra randsegment: nämligen linjen
som sammanbinder noderna 3 och 5. I detta fall
skulle e-matrisen alltså ha två extra kolonner,
motsvarande de två triangelsidor som ligger på detta, inre, randsegment.
Detta randsegment är ett exempel på en så kallad inre rand.)
Enligt figuren tänker vi oss att vi har fem stycken
randsegment: randsegment nummer 1 är "golv"; randsegment
nummer 2 och 5 är "väggar"; randsegment nummer
3 och 4 utgör "taket". Eftersom det ligger
två stycken triangelsidor på randsegment nummer 1,
och endast en triangelsida på vart och ett av de övriga fyra
randsegmenten, blir nedges = 2 + 1 + 1 + 1 + 1 = 6, varför
e blir en 7 x 6-matris. Notera också (se figur) att
vi har infört en orientering av varje randsegment. Den är vald
så att området, Omega, hela tiden ligger till vänster om dig
då du "promenerar" längs randen i orienteringens riktning.
Vi inför nu (godtyckligt) följande numrering av triangelsidorna som
ligger på ett randsegment:
1. sidan som sammanbinder nod 1 och nod 6
2. " 6 " 2
3. " 2 " 3
4. " 3 " 4
5. " 4 " 5
6. " 5 " 1
För var och en av dessa sex sidor skall motsvarande kolonn i
e innehålla följande information:
rad 1: nodnummer för sidans "start-nod"
rad 2: nodnummer för sidans "slut-nod"
(Vilken som är "start-nod" och vilken som är "slut-nod"
hänger förstås samman med orienteringen hos det rand-
segment varpå sidan ligger.)
rad 3: parametervärde i sidans "start-nod"
rad 4: parametervärde i sidans "slut-nod"
(Dessa använder vi oss inte av men om du är nyfiken
så fungerar det så här: varje randsegment antas vara
parametriserat med en parameter som är proportionell
mot båglängden på ett sådant sätt att den "första" noden
på randsegmentet har parametervärdet 0 och den "sista" har
parametervärdet 1. När du rör dig längs randsegmentet i
orienteringens riktning växer alltså parametervärdet från
0 till 1: t.ex. är det 0.5 när du gått halvvägs!)
rad 5: numret på det randsegment varpå sidan ligger
rad 6: numret på delområdet till vänster om sidan
rad 7: numret på delområdet till höger om sidan
(När du rör dig i orienteringens riktning.)
Vi kan därmed skapa e enligt:
>> e = zeros(7, 6); % initiera e
>> e(:, 1) = [1; 6; 0; 0.5; 1; 1; 0] % triangelsida 1
>> e(:, 2) = [6; 2; 0.5; 1; 1; 1; 0] % triangelsida 2
Mata nu själv in data för övriga fyra
triangelsidor i e. Notera att delområdet till vänster
alltid har nummer 1 medan "delområdet" till höger,
utanför Omega, har nummer 0. Rad 3-4
kan du i princip sätta till vad som helst: de används som sagt
ej i våra program!
Nu har du skapat matriserna p, t, och e,
vilka beskriver trianguleringen av Omega, och vilka behövs
som indata till din assemblerare. Men innan du anropar denna måste
du även specificera data till problemet i de funktionsfiler
som assembleraren i sin tur anropar. I husproblemet så är
diffusionskoefficienten och källtermen konstanta (=1) i
hela Omega, men tänk på att vi har olika randdata på
"golv" (randsegment 1) och "väggar och tak" (randsegment
2-5). Var mycket noggrann när du gör detta, och glöm
aldrig bort att kontrollera samtliga "data-filer" innan du
startar en ny beräkning.
Anropa nu din(a) assemblerare (obs: inte din "solver"; vi skall
inte lösa differentialekvationen, endast assemblera matriser och vektorer),
och beräkna 7x7-matriserna
M (massmatris), A (styvhetsmatris)
och K ("randbidragsmatris"),
samt 7x1-vektorerna F (lastvektor)
och G ("randbidragsvektor").
Jämför med resultaten från din handräkning!
A, F och G bör stämma
överens exakt.
Om du i din kod för att beräkna
dubbelintegralerna i massmatriselementen
använt kvadratur baserad på integrandens värde
i triangelsidornas mittpunkter bör också M bli exakt, men
om du använt nodkvadratur får du istället den lumpade
massmatrisen; prova i detta fall att för varje rad i din
handräknade massmatris addera samtliga element i denna rad,
och kontrollera därefter att summan stämmer
överens med diagonalelementet i
motsvarande rad i den lumpade massmatrisen.
Den exakta och den lumpade
massmatrisen ser ut som följer:
/ \
| |
| 1/24 0 0 0 1/96 1/96 1/48 |
| 1/24 1/96 0 0 1/96 1/48 |
| 1/24 1/96 0 0 1/48 |
M = | 1/24 1/96 0 1/48 |
| symm. 1/24 0 1/48 |
| 1/24 1/48 |
| 1/8 |
| |
\ /
/ \
| |
| 1/12 0 0 0 0 0 0 |
| 1/12 0 0 0 0 0 |
| 1/12 0 0 0 0 |
M_lump = | 1/12 0 0 0 |
| symm. 1/12 0 0 |
| 1/12 0 |
| 1/4 |
| |
\ /
För att få ut
K exakt från din assemblerare krävs att du använder
antingen Simpson's formel eller Gauss' 2-punktsformel
vid beräkning av kurvintegralerna över randen till Omega.
Om du inte modifierat denna del av programmet
i den kod du fått utgå ifrån, är det troligt att
trapetsregeln används och i dessa fall blir
alltså
K ej exakt. Titta efter i din assemblerare vilken
kvadraturregel som är "i bruk",
och jämför sedan med relevant variant nedan:
/ \
| |
| 1/6 0 0 0 1/12 0 0 |
| 1/6 1/12 0 0 0 0 |
| (1/6)+1/(3*sqrt(2)) 1/(6*sqrt(2)) 0 0 0 |
K = | 2/(3*sqrt(2)) 1/(6*sqrt(2)) 0 0 |
| symm. (1/6)+1/(3*sqrt(2)) 0 0 |
| 0 0 |
| 0 |
| |
\ /
/ \
| |
| 1/4 0 0 0 0 0 0 |
| 1/4 0 0 0 0 0 |
| (1/4)+1/(2*sqrt(2)) 0 0 0 0 |
K_trap = | 1/sqrt(2) 0 0 0 |
| symm. (1/4)+1/(2*sqrt(2)) 0 0 |
| 0 0 |
| 0 |
| |
\ /
/ \
| |
| 1/8 0 0 0 1/8 0 0 |
| 1/8 1/8 0 0 0 0 |
| (1/8)+1/(4*sqrt(2)) 1/(4*sqrt(2)) 0 0 0 |
K_mid = | 1/(2*sqrt(2)) 1/(4*sqrt(2)) 0 0 |
| symm. (1/8)+1/(4*sqrt(2)) 0 0 |
| 0 0 |
| 0 |
| |
\ /
Extra tester du kan göra:
1. Litet hus. Prova att förminska huset med en faktor två (i
längdskala) genom kommandot >> p = p/2! Räkna ut nya matriser
och vektorer för det lilla huset (i Matlab). Jämför nu den gamla
och den nya massmatrisen. Hur skiljer de sig åt? Förklara! Gör samma
sak med styvhetsmatrisen. Kommentar?
2. Radsummor i M. Beräkna kolonnvektorn med radsummor
av elementen
i massmatrisen, d.v.s., kolonnvektorn där elementet i rad i
är summan av samtliga element i motsvarande rad i M.
(Jfr. lumpad massmatris.)
Tips: Använd kommandot >> radsummor = sum(M, 2). Jämför
med lastvektorn F. Kan du förklara varför dessa är lika
i detta fall (med f=1)?
Ge en geometrisk tolkning av elementen i radsummor som
volymer.
Ledtråd: Summan av alla
tältfunktioner är den funktion som är identiskt lika med 1.
3. Arean av Omega. Räkna nu ut summan av samtliga element i
kolonnvektorn från uppgift 2. Tips: Använd
kommandot >> sum(radsummor, 1). Jämför resultatet med arean
av Omega. Förklara!
4. Radsummor i A. Beräkna kolonnvektorn med radsummor
av elementen i styvhetsmatrisen, analogt med uppgift 2. Vad
blir resultatet? Varför?
|