 |
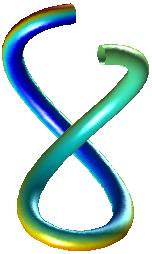 |
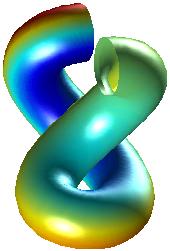 |
Matlab, kurvor och ytor
Syftet med denna laboration är att Du skall repetera lite Matlab samt lära Dig hantera kurvor och ytor.
Matlab är ett utmärkt hjälpmedel när Du löser de övningar i övningsboken som kräver att komplicerade områden i planet eller rummet skall ritas upp. Detta är inte alltid så lätt att göra för hand.
Mindre än lika med skrivs <=.
Matlabkoden läggs lämpligen i en m-fil.
Redovisa Matlabkod och
plottar.
Matlab-tips finns
under FAQ i marginalen.
 Används Matlabs
Används Matlabs plot-kommando
för
att rita upp randen till följande mängd i R2:
M ={ (x, y): |x| <= 3 , |y| <= x2 + 1 }.
Använd
fill-kommandot för att rita både randen och det
inre
av M (dvs. fyll området med t.ex. röd färg).
Här är några andra lämpliga
kommandon.
figure, hold, axis,
linspace, .^ (eller .*),
xlabel, ylabel, title.
En lämplig rubrik kan skapas med kommandot::
title('\{ (x, y) : |x| \leq 3, |y| \leq x^2 + 1
\}', ...
'Fontsize', 12, 'Fontweight', 'Bold')
plot3) men de är svårtolkade
eftersom
det är svårt att få någon djupverkan i plotten.
En
plot med några kurvor ser gärna ut som ett
ståltrådsnystan
på lite avstånd, vilket gör det omöjligt att
avgöra
vilken kurva som ligger bakom/framför en annan. För att
göra
bilden enklare att tolka ritar man ibland kurvorna som rör eller
band.
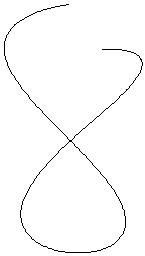
Jämför bilderna nedan, som visar hur en kurva kan
visualiseras
på olika sätt. I rörbilderna används även
färg
och belysning. I denna kurs kommer vi att rita kurvor som i bilden
längst
till vänster.  |
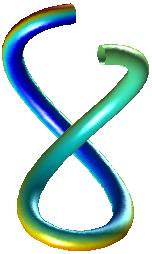 |
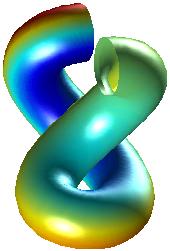 |
 Rita en spiral enligt
vänstra bilden nedan. Spiralen
slingrar sig runt enhetssfären. För att Du tydligare skall se
hur
bilden är konstruerad har jag i den andra figuren ritat
sfären
(denna bild behöver Du inte rita). Rita också den tredje
bilden
(en tätare spiral). Ledning.
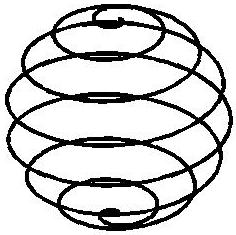
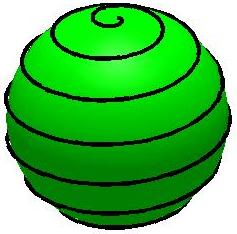
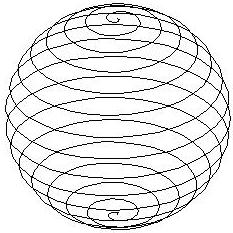
Rita en spiral enligt
vänstra bilden nedan. Spiralen
slingrar sig runt enhetssfären. För att Du tydligare skall se
hur
bilden är konstruerad har jag i den andra figuren ritat
sfären
(denna bild behöver Du inte rita). Rita också den tredje
bilden
(en tätare spiral). Ledning.
 |
 |
 |
Man kan variera linjetjockleken så här:
plot3(x, y, z, 'Linewidth', 4) % eller
någon annan lämplig
tjocklek
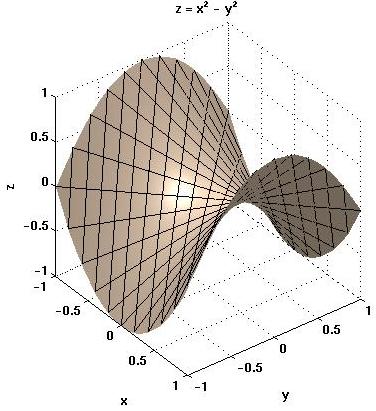
Den hyperboliska paraboloiden (en sadelyta) har den egenskapen att man kan dra räta linjer som ligger i ytan. Detta är ett sätt att konstruera ytan. Se bilden till vänster där ytan z = x2 - y2 och delar av några räta linjer är uppritade. I den högra bilden är endast linjerna uppritade.
 |
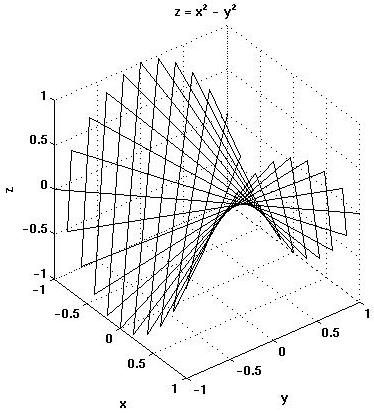 |
 Rita den högra bilden. Jag vill ha ett
bevis för att linjerna
verkligen ligger i ytan. Det räcker
inte med en plot. Ledning.
Rita den högra bilden. Jag vill ha ett
bevis för att linjerna
verkligen ligger i ytan. Det räcker
inte med en plot. Ledning.
Antag att vi vill rita punktmängden (ytan)
M = {(x, y, z): z = f(x, y), (x, y) tillhör D} där D = {(x, y): xmin <= x <= xmax, ymin <= y <= ymax }
så D är ett rektangulärt område i x-y-planet.
Ett sätt att göra detta i Matlab är att
först bilda ett
rutnät (grid) i mängden D. För att förstå hur
detta
fungerar, exekvera följande Matlabrad och inspektera X
och Y.
[X, Y] = meshgrid(-1:0.5:1, 1:4)
Antag nu att matrisen F, innehåller
funktionsvärdena,
f(X(j, k), Y(j, k)). Kommandot
mesh(X, Y, F)
ritar då en approximation, i form av ett nät, av ytan. Ju bättre upplösning man har i rutnätet desto jämnare yta får man. Samtidigt tar matriserna mer plats och grafiken blir slöare (om man vill snurra på ytan till exempel). Tänk också på att om Du fördubblar antalet punkter i x- och y-led så innehåller matriserna fyra gånger så många element.
Matrisen F kan byggas upp med loopar, men ett snabbare och enklare sätt är att använda elementvisa operationer. Testa t.ex. följande rader:
x = linspace(-1, 1, 10); % Dålig
upplösning
y = linspace(0, 2, 10);
[X, Y] = meshgrid(x, y);
F = X.^2 .* Y; % Observera
punkterna
figure
% Skapa nytt fönster
mesh(X, Y, F)
rotate3d %
Slå
på rotation
figure
% (kan klicka på rotationspilen också)
surf(X, Y, F) % Ett annat
sätt
att rita ytan
shading interp %
Jämna ut
färgerna (löst uttryckt)
rotate3d
Regnbågsfärgen i ovanstående bild kan ändras (man kan ha en färg och lägga på belysning t.ex.) men vi tar inte upp detta i denna kurs.
 Rita funktionsytan som ges av z =
sin(x y), |x|
<= 2, |y| <= 2. x y står för x multiplicerat med
y.
Rita funktionsytan som ges av z =
sin(x y), |x|
<= 2, |y| <= 2. x y står för x multiplicerat med
y.
Antag att vi vill rita mängden, { (x, y, z): x2
+
y2 + z2 = 1, 0 <= z }, dvs. en halvsfär.
Om
vi gör som ovan med D = { (x, y): |x| <= 1, |y| <= 1 }
får
vi några problem. Det första är att sqrt(1 -
X.^2 -
Y.^2) kommer att innehålla komplexa tal (som inte ritas
ut),
men figuren blir inte alls bra. Vi kan fixa det komplexa talen med
följande
kodsegment:
Z2 = 1 - X.^2 - Y.^2;
Z2(Z2 < 0) = 0; % Sätt alla
element
< 0 till 0.
surf(X, Y, sqrt(Z2))
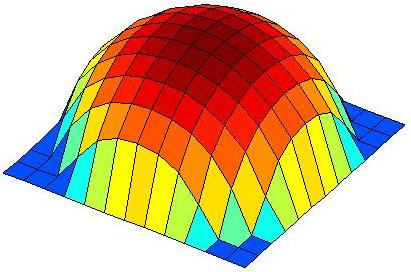
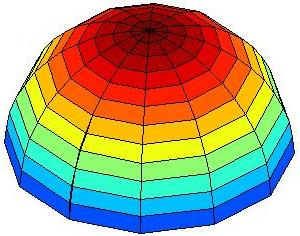
Detta ger dock samma bild (den till vänster nedan)
som när vi
räknar med komplexa tal. För att konstruera den högra,
snyggare,
bilden gjordes ett koordinatbyte till polära koordinater och ett
grid
i de nya koordinaterna (ungefär som sid. 31-32 i läroboken).
Slutligen
plottades halvsfären med surf.
 |
 |
Ovanstående förfarande kan generaliseras genom att byta till andra koordinater. Om vi vill rita en del av en ellipsoid är det lämpligt med elliptisk-polära koordinater, x = a r cos(v), y = b r sin(v). a och b är konstanter (bestäms av ellipsoiden). I sfärfallet är a = b = 1.
 Använd elliptisk-polära
koordinater för
att göra en snygg plot av följande mängd i R3:
{ (x, y, z): z = x2 / 4 + y2 / 9 + 1, z <= 2
}.
Rita även några av ytans nivåkurvor. Detta kan man
göra
i samma plot med kommandot
Använd elliptisk-polära
koordinater för
att göra en snygg plot av följande mängd i R3:
{ (x, y, z): z = x2 / 4 + y2 / 9 + 1, z <= 2
}.
Rita även några av ytans nivåkurvor. Detta kan man
göra
i samma plot med kommandot surfc eller i ett annat
fönster
med kommandot contour. Testa båda! Slå
också
på ett grid, grid on, i den andra plotten. Ledning.
 Rita två lämpliga ytor i samma
diagram för
att få en uppfattning om hur följande mängd ser ut:
Rita två lämpliga ytor i samma
diagram för
att få en uppfattning om hur följande mängd ser ut:
{ (x, y, z): x2 / 4 + y2 / 9
<= z <= (1
- x2 - y2)1/2, 0 <= y
}
Var i er plot finns mängden (beskriv
i ord till exempel)?