Exempel 3

Flera, lite besvärligare, bivillkor

Följande exempel kommer inte från en föreläsning och det är inkluderat bara för att visa hur man kan vara tvungen att formulera om sitt problem och hur man paketerar flera bivillkor.

Problem:
Låt f(x1, x2) = 0.4 sin(3 x1 x2 + x2) + 1. Minimera f(x1, x2) då (x1, x2) tillhör området som ges av |x1| + |x2| <= 1 och |x2| <= x1^2.

Steg 1: karakterisera objektfunktion och bivillkor
Objektfunktionen är ickelinjär. Vi får samma minimipunkt (men inte samma minvärde) med sin(3 x1 x2 + x2), men vi behåller ursprungsformuleringen (0.4 och 1 är valda så att plotten skall bli snygg). Bivillkoren liknar inte de i våra föregående exempel. Vi vill avlägsna beloppen eftersom de ger hörn. I dokumentationen för fmincon står nämligen:

fmincon is a gradient-based method that is designed to work on problems where the objective and constraint functions are both continuous and have continuous first derivatives. function with continuous first and second derivatives because the algorithm uses gradient-based methods.

Steg 2: skriv objektfunktion och bivillkor på standardform
Objektfunktionen är redan på standardform. Bivillkoren kräver lite arbete dock. En av övningarna i Adams går ut på att rita mängden som definieras av |x1| + |x2| <= 1, och det visar sig bli en roterad kvadrat med kantlinjer x1 + x2 = 1, -x1 + x2 = 1, -x1 - x2 = 1 samt x1 - x2 = 1. Efter lite tänkande ser man att villkoren blir:

x1 + x2 <= 1
-x1 + x2 <= 1
-x1 - x2 <= 1
x1 - x2 <= 1

De ickelinjära villkoren kan vi skriva som två villkor x2 <= x1^2 och -x2 <= x1^2. Standardformen lyder c(x) <= 0, där c är en funktion som definierar ett bivillkor, så i vårt fall:

-x1^2 + x2 <= 0
-x1^2 - x2 <= 0

Steg 3: förpackning; vi inför de vektorer och matriser som behövs för att definiera objektfunktion och bivillkor
Vi inför först x som vektorn som lagrar variablerna, x1 och x2.

Olikhetsbivillkoren definieras av en matris A och en kolonnvektor B, där A * x <= B, en rad per bivillkor. Matrisen A har fyra rader (fyra bivillkor) och två kolonner (två variabler) och ser ut som följer:

	[	1	1	]		[	1	]
A =	[	-1	1	]	B =	[	1	]
	[	-1	-1	]		[	1	]
	[	1	-1	]		[	1	]

Det ickelinjära bivillkoret definieras via en funktion, precis som i föregående exempel, [in_eq, eq] = constr_fun(x). Skillnaden är att vi nu har olikhetsbivillkor och dessutom två stycken. Vi returnerar avvikelserna som en kolonnvektor.

in_eq = [-x(1)^2+x(2); -x(1)^2-x(2)];

Eftersom vi inte har något likhetsbivillkor sätter vi eq till en tom variabel []. Om vi hade flera likhetsbivillkor hade vi analogt returnerat en vektor av avvikelser från bivillkoren.

Steg 4: skriv Matlabkoden
Jag har valt att lägga de tre rutinerna i en fil .

function ex3
A    = [1 1; -1 1; -1 -1; 1 -1]; % fyra linjära olikhetsbivillkor
B    = [1; 1; 1; 1];

A_eq = [];                       % inget linjärt likhetsbivillkor
B_eq = [];

LB   = [];                       % inga enkla gränser
UB   = [];

x_guess = [-0.1; 0.6];

[x_opt, obj_val] = fmincon(@obj_fun, x_guess, A, B, A_eq, B_eq, LB, UB, @constr_fun)

function obj_val = obj_fun(x)
obj_val = 0.4 * sin(3 * x(1) * x(2) + x(2)) + 1;

function [in_eq, eq] = constr_fun(x)
in_eq = [-x(1)^2 - x(2); -x(1)^2 + x(2)]; % ickelinjära olikhetsbivillkor
eq    = [];                                % inget ickelinjärt likhetsbivillkor

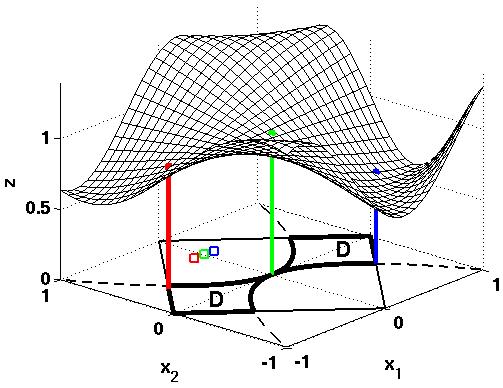
Följande bild visar några av problemets egenskaper. De tunna linjerna i x1-x2-planet visar randen till |x1| + |x2| <= 1 och de streckade linjerna visar analogt randen för |x2| <= x1^2. De tjocka linjerna visar randen för D, det område vi minimerar över. Beroende på var man startar hittar rutinen olika punkter. Om vi startar i den röda kvadraten hamnar vi i den punkt som markerats med en röd stolpe (jag har dragit upp stolpen till ytan, så att man enklare skall se var på ytan man hamnar). Notera att punkten ligger på randen (utan bivillkor hade vi inte haft lokalt minimum här). Analogt för de andra kvadraterna.