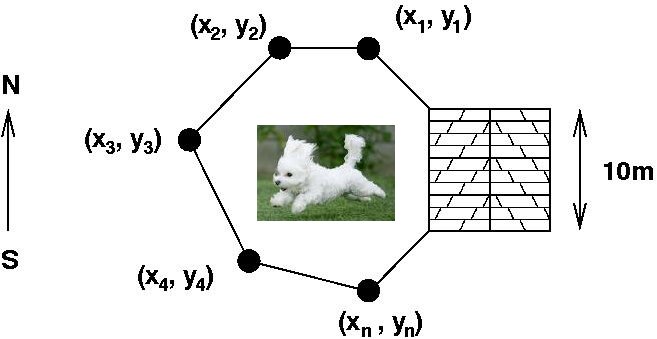
Optimering

I denna lab kommer Du att använda en av Matlabs optimeringsrutiner för att räkna ut formen på en inhägnad, en hundgård säg. Själva beräkningsuppgiften är inte så realistisk, men de moment du kommer att utföra i labben är dock mycket realistiska. Optimering används ofta i tillämpningar. En fördel med uppgiften är också att den är lätt att förstå och eftersom man kan rita upp formen på stängslet kan man också avgöra om man har hittat en vettig lösning.

Du har 100 m stängsel och 30 stängselstolpar. Uppgiften går ut på att bestämma stolparnas positioner så att inhägnadens area maximeras. Du kommer att lösa tre varianter av problemet. I slutet av labben finns några exempel på hur man använder Matlab-rutinen fmincon.

Lägg märke till att:
Här ett exempel där vi har n = 5 stolpar, numrerade moturs. Bilden är inte skalenlig.

Inhägnad


 
Ledning: för att räkna ut arean kan man använda Greens formel (som kommer i slutet av kursen, men som du inte behöver förstå för att kunna göra denna lab). Se avsnittet "GPS och areaberäkningar" i föreläsningsanteckningarna, formeln som är märkt med spader. Man kan ta bort absolutbeloppet om man numrerar punkterna moturs. Här är en Wikipedialänk med väsentligen samma formel (det är underförstått att (x1, y1) = (xn, yn) i Wikipedia-formeln) .
Observera att numreringen av (x, y)-koordinaterna i formeln inte svarar direkt mot stängselstolparnas numrering. Du måste alltså anpassa formeln till labben! Här några exempel på hur formeln fungerar. Mina exempel är inte anpassade till labben.
Fråga  Använd rutinen fmincon för att bestämma stolparnas positioner. Se till att hela stängslet används (bivillkor!). Skriv ut den optimala arean och plotta stolparnas positioner och stängsel som i plotten ovan. Det räcker att du ritar husväggen som en streckad linje. Låt husväggens ändpunkter ha koordinaterna (0, -5) respektive (0, 5). Bifoga Matlabkod.

Ledning och krav:
Fråga  Vi har samma situation som ovan, men  stängslet utsträckning hindras av två vägar som ligger väster om huset. Ekvationerna för de delar av vägarna som ligger längst österut (högra vägrenarna) är x + y + 20 = 0 respektive y - x - 40 = 0. Stängslet måste ligga till höger (eller på) dessa linjer. Skriv ut arean och plotta som ovan. Rita även ut vägarna (bivillkoren). Bifoga Matlabkod.

Ledning: man skulle kunna slå ihop de två vägarna till en väg (den sammansatta vägen ser ungefär ut som bokstaven V roterad 90 grader medurs), men motsvarande bivillkor blir dels ickelinjärt och dessutom introducerar man ett hörn (ingen derivata). Detta kan orsaka problem för en optimeringsrutin, så behandla vägarna som separata bivillkor.
Fråga  En nackdel med lösningen ovan är att avståndet mellan stolparna varierar. Det gör att vissa stolpar utnyttjas dåligt (står för tätt) och andra står för glest (stängselnätet hänger ner). Så, utgå från föregående uppgift, men lägg på bivillkor så att avståndet mellan konsekutiva stolpar är lika, kalla detta avstånd L. Avståndet från övre vänstra husknuten till första stolpen skall också vara L liksom avståndet mellan sista stolpen och den nedre vänstra husknuten. Skriv ut arean och plotta som ovan. Bifoga Matlabkod.

Ledning:

Allmän ledning till alla tre uppgifterna. Jag har avsiktligt inte talat om hur du skall formulera bivillkor och objektfunktion i de tre deluppgifterna. En väsentlig del av labben är nämligen att lära sig detta, då sådan kunskap krävs i riktiga optimeringstillämpningar. Nu kan kanske Matlabs online-hjälp vara lite svår att tränga igenom, så jag har tillhandahållit några lösta exempel, där jag visar hur fmincon kan användas. Två av exemplen kommer från föreläsningar (där vi handräknade fram lösningen). Inget av exemplen passar precis med någon av labuppgifterna (avsiktligt!), men följande länkar innehåller tillräckligt med byggstenar för att du skall kunna lösa labben. Exemplen innehåller också annat matnyttigt som behövs när man löser verkliga problem.

Det är stor risk att du måste tillåta rutinen att utföra fler funktionsberäkningar än vad som är standard, så missa inte länken "Saker som kan gå fel" nedan.

Back