Exempel 4

Diverse svårigheter man kan råka ut för

Optimeringsproblem kan vara svåra att formulera korrekt, men även korrekt formulerade problem kan ge fmincon bekymmer. Här följer exempel på några av de svårigheter man kan råka ut för.

Det är viktigt att formulera problemet korrekt. Det är t.ex. viktigt att använda rätt på tecken i bivillkoren, så att man inte får motsägelser. Antag att vi vill minimera x (en skalär variabel) när x <= 1 och x >= 2. Detta är givetvis omöjligt och det är uppenbart att vi har gjort ett fel. Detta är nu inte alltid så lätt att upptäcka i riktiga problem, där man kan ha tusentals bivillkor (som dessutom inte är enkla gränser). Samma problem kan inträffa med likhetsbivillkor, x = 2 och x = 3 t.ex.

fmincon ger ett felmeddelande i dessa fall:

Optimization terminated: no feasible solution found.

"A feasible solution" (en tillåten lösning, tillåten punkt) är en punkt som uppfyller bivillkoren, och rutinen hittar ingen sådan punkt. Man kan få detta felmeddelande även om det finns tillåtna punkter, men där startpunkten ligger så långt ifrån en tillåten punkt, att rutinen inte hittar fram. Det är viktigt med bra startvärden, men det kan vara svårt att hitta en startgissning som uppfyller bivillkoren. Det brukar dock räcka att man hittar en startgissning som inte bryter alltför mycket mot bivillkoren.

Ibland glömmer man bivillkor. Vi minimerar kanske en massa (vikt) och för oss är det självklart att massan skall vara ickenegativ. En optimeringsrutin har ju inte några sådana fördomar, utan den kan mycket väl ge oss ett negativt resultat.

Vi kan också råka ut för att iterationerna skenar iväg. Säg att vi minimerar f(x) = x^3 - 10 x. Funktionen har ett lokalt minimum för x = sqrt(10/3) (och ett lokalt maximum för -sqrt(10/3)), men den saknar globalt minimum. Om vi startar till vänster om -sqrt(10/3) kommer rutinen att producera alltmer negativa iterander. För att undvika oändliga loopar finns en begränsning på antalet funktionsberäkningar (av objektfunktionen) rutinen får utföra (standardvärdet är 100 * antalet variabler), och rutinen bryter med felmeddelandet:

Maximum number of function evaluations exceeded; increase OPTIONS.MaxFunEvals.

När vi arbetar med objektfunktioner som inte är nedåt begränsade, kan det vara lämpligt att införa enkla gränser på variablerna. Om vi avgränsar en kompakt mängd existerar ett minsta värde (vår objektfunktion är ju kontinuerlig). Detta minsta värde är nog ointressant, men vi riskerar inte att rutinen utför onödigt många funktionsberäkningar. Man måste sedan inspektera det resultat som fmincon producerat för att se om det är av något intresse.

Vi kan få ovanstående felmeddelande utan att någonting är fel. Det kan vara så att problemet är så pass svårt att rutinen får ta många steg för att hitta fram. Det är då möjligt att tillåta rutinen att utföra fler beräkningar. Här ett exempel:

   min x1 över (x1, x2)
   då -x1 + 16 (x2 - x1^2)^2 = 0
   och -5 <= x1, x2 <= 5

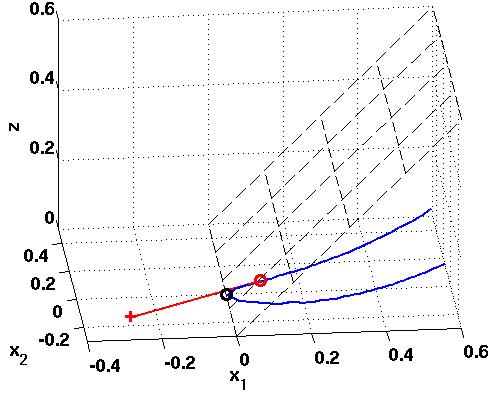
Vi har en väldigt enkel linjär objektfunktion, men ett lite besvärligt ickelinjärt likhetsbivillkor. Även om vi startar med en tillåten punkt, så har fmincon problem att hitta minimum (x1, x2) = (0, 0). Här en bild av objektfunktion och olikhetsbivillkor. Startgissningen (x1, x2) är ungefär (0.1, 0.089) (avvikelsen i bivillkoret är -4e-17, vilket väsentligen är noll).

Den streckade ytan utgör en del av objektfunktionen och den blå kurvan är en del av olikhetsbivillkoret. Den svarta ringen markerar minimum och den röda startpunkten. Rutinen tar ett alldeles för långt förstasteg och hamnar i det röda krysset och sedan går rutinen ännu mera vilse. Det är först när den slår emot de enkla gränserna som det tar stopp. Om jag ger rutinen flera funktionsberäkningar hittar den tillbaks efter 252 funktionsberäkningar.

Så här ökar man antalet funktionsberäkningar (jag påstår inte att 500 räcker i labben):

options = optimset; % skapa postvariabeln options
options.MaxFunEvals = 500; % sätt datamedlemmen MaxFunEvals till 500 (till exempel)
% skicka med options sist i anropet av fmincon
[x_opt, obj_val] = fmincon(@obj_fun, x_guess, A, B, A_eq, B_eq, LB, UB, @constr_fun, options)

En kortform för de två första raderna är:
options = optimset('MaxFunEvals', 500);

Du skulle också kunna få felmeddelandet "Maximum number of iterations exceeded; increase OPTIONS.MaxIter". Öka då datamedlemmen MaxIter (om du tror att din kod är korrekt). Observera då att optimset skall anropas en gång, så t.ex.
options = optimset('MaxFunEvals', 500, 'MaxIter', 1000);

fmincon är inte bara en metod utan rutinen kan växla mellan olika alternativ. Ibland är inte ett av dessa alternativ tillgängligt (för det aktuella problemet), varför rutinen ger en varning.

Warning: Large-scale (trust region) method does not currently solve this type of problem, using medium-scale (line search) instead.

Detta är alltså en upplysning och inte resultatet av något fel vi gjort. Genom att välja bort den icke tillgängliga metoden slipper vi meddelandet:

options.LargeScale = 'off';