MATEMATIK, Chalmers tekniska högskola
Lösningar till tentamen i Matematik K, del D (TMA151) 2000-05-27.

1. Vi har att $E=\{(x,y,z): 0<x^2+y^2<1, \;\; 0<z<1\}.$ Dvs $E$ är en cylinder.
$$I=\int\!\!\!\!\int\!\!\!\!\int_E \sin( \frac{\pi}{2} z) \, d......=\int_0^1 \sin( \frac{\pi}{2} z) dz \int\!\!\!\!\int_D dx\,dy,$$


där $D$ är enhetsskivan $\{ 0<x^2+y^2<1\}$. $D$ har arean $\pi$. Därför är

$$I=\pi\int_0^1 \sin( \frac{\pi}{2} z) dz=\pi\biggl[-\frac{2}{\pi}\cos( \frac{\pi}{2} z)\biggr]_0^1=2.$$
2. Låt oss kalla den sökta potentialen för $\varphi(x,y,z)$. Vi vill alltså hitta en sådan skalärfunktion så att
$$\mbox{grad} \varphi = \mathbf{F}=(z^2-2xe^{x^2+y^2}, -2ye^{x^2+y^2}-z^3, 2zx-3z^2y).$$


Vi har att $\varphi_x=z^2-2x e^{x^2+y^2}$, vilket ger att $\varphi=z^2x-e^{x^2+y^2}+g(y,z)$. Partiell derivering med avseende på$y$ ger $\varphi_y=-2y e^{x^2+y^2}+g_y(y,z)$. Jämförelse med andra komponenten i $\mathbf{F}$ ger att $g_y(y,z)=-z^3$. Därför måste $g(y,z)=-z^3y+h(z)$. Derivering med avseende på $z$ och jämförelse med $\mathbf{F}$ ger tillslut att $h'(z)=0$. Vi har då att $h$ är konstant och vi kan till exempel välja den konstanten till $0$. Detta ger oss tillslut att en potential till $\mathbf{F}$ kan skrivas som

$$\varphi(x,y,z)=z^2x-e^{x^2+y^2}-z^3y.$$
3. a) Villkoret $\lim_{x \rightarrow 0} \frac{R(x)}{x^3}=0$ betyder att $R(x)=x^3 o(1)$. Vi använder oss av tabellen och utvecklar på, innifrån och ut, tills felet är $x^3 o(1)$.
$$\cos x = 1-\frac{x^2}{2}+x^3o(1), \; \mbox{ detta insatt i utvecklingenför } \ln (1+x) \mbox{ ger då }$$ $$\ln(\cos x )= -\frac{x^2}{2}+x^3o(1) \mbox{ vilket slutligen ger oss }$$ $$\arctan ( \ln(\cos x ))= -\frac{x^2}{2}+x^3o(1).$$

b) Från a) och Maclaurinutveckling av $\sin x$ har vi att

$$\lim_{x \rightarrow 0} \frac{f(x)+\frac{x^2}{2}}{\sin x -x}=......\lim_{x \rightarrow 0} \frac{ o(1)}{\frac{1}{3!}+x^3 o(1)}=0.$$
4. Greens formel ger att
$$\oint_{\partial \Omega} x \ln y \, dx=\int\!\!\!\!\int_\Omega......, dy=-\int_1^2 x \int_{e^x}^{e^{x^3}} \frac{1}{y} \, dy\, dx=$$ $$=-\int_1^2 x(x^3-x) \, dx= \ldots=\frac{-58}{15}.$$
5. Fjäderns massa ges av följande integral.
$$\int_{t=0}^{6\pi} \mbox{\lq\lq densiteten''}\, ds.$$


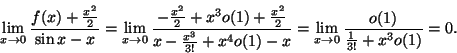
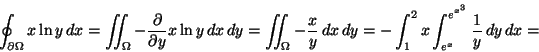
Densiteten är $\vert\mathbf{r}(t)\vert^2$, där $\mathbf{r}(t)=(4\cos t, 4 \sin t, 3t)$. Detta ger oss att vi kan skriva densiteten som

$$\vert\mathbf{r}(t)\vert^2= (4^2(\cos^2 t + \sin^2 t)+3^2t^2)= (16+9t^2).$$

Båglängdselementet, $ds$, får en ännu finare form.

$$ds= \sqrt{\dot{r}_x^2+\dot{r}_y^2+\dot{r}_z^2}=\sqrt{4^2(\cos^2 t + \sin^2 t)+3^2}\, dt=\sqrt{16+9}\, dt=5\, dt.$$

Vi kan nu beräkna fjäderns massa:

$$\int_{0}^{6\pi} (16+9t^2) 5 \,dt=5 \int_{0}^{6\pi} 16+9t^2\, ......+3t^3\biggr]_0^{6 \pi}= 30\pi(16+108\pi^2) \mbox{ massenheter.}$$
6. Villkoret $y(t)=\frac{t^2}{2} \mbox{ för } t<0$, ger att $y(0^-)=y'(0^-)=0$ och $y''(0^-)=1$. Vi kan nu Laplacetransformera båda leden med hjälp av L07 och L19 i tabellen. Detta ger följande algebraiska uttryck.

$$Y(s)=\frac{e^{-s}+1}{s^3-1}.$$ (1)

Vi ser direkt att $s=1$ är en rot till $s^3-1=0$. Polynomdivision ger då att $s^3-1=(s-1)(s^2+s+1)$.

Vi kan nu göra följande ansats för partialbråksuppdelning.

$$\frac{1}{s^3-1}=\frac{A}{s-1}+\frac{Bs+C}{s^2+s+1}.$$


Detta ger så småningom att $A=\frac{1}{3}, B=-\frac{1}{3}$ och $C=-\frac{2}{3}$. Vi har då att

$$\frac{1}{s^3-1}=\frac{1}{3} \frac{1}{s-1}-\frac{1}{3}\frac{s+......1}{2})+\frac{3}{2}}{(s+\frac{1}{2})^2+(\frac{\sqrt{3}}{2})^2}=$$ $$=\frac{1}{3} \frac{1}{s-1}-\frac{1}{3}\frac{(s+\frac{1}{2})}......\frac{\sqrt{3}}{2}}{(s+\frac{1}{2})^2+(\frac{\sqrt{3}}{2})^2}.$$


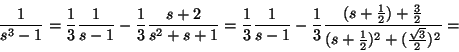
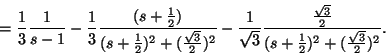
Med hjälp av L14, L15, L16 och L04, får vi den inversa transformen och döper den till $f(t)$.

$$f(t)=\mathcal{L}^{-1}(\frac{1}{s^3-1})=\frac{1}{3} e^t-\fra......-\frac{1}{\sqrt{3}} e^{-\frac12 t} \sin(\frac{\sqrt{3}}{2} t).$$ (2)

Vi utnyttjar nu $f(t)$ tillsammans med L05, där $T=1$, för att få: $$\mathcal{L}^{-1}(\frac{e^{-s}}{s^3-1})=f(t-1)\theta(t-1).$$

Vi får då från ekvation (1) att

$$y(t)=f(t-1)\theta(t-1)+f(t),$$


för $t>0$. Vi justerar nu denna lösning med hjälp av stegfunktionen $\theta(t)$ för att få en lösning som också gäller för negativa $t$.

$$y(t)=f(t-1)\theta(t-1)+f(t)\theta(t) +\frac{t^2}{2}\theta(-t),$$


där $f(t)$ är definerad i (2).

7. Låt $a$ vara det vertikala från $A$ till vattenytan, $b$ avståndet från$B$ till vattenytan och $c$ det horisontella avståndet mellan $A$ och$B$. Se figur!
Vi har då sambandet att

$$c=a \tan \theta_1 +b \tan \theta_2.$$ (3)

Vi vill minimera tiden för laserstrålen att gå mellan $A$ och $B$. Tiden fås genom följande funktion. $$f(\theta_1, \theta_2)= \frac{a}{v_1 \cos \theta_1} +\frac{b}{v_2 \cos \theta_2}.$$


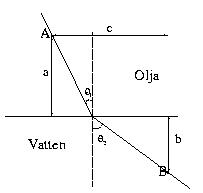
Bivillkoret i (3) ger oss

$$u(\theta_1, \theta_2)=a \tan \theta_1 +b \tan \theta_2-c.$$

Rangmetoden ger oss att

$$\mbox{Rang } \frac{D(f,u)}{D(\theta_1,\theta_2)}= \mbox{ Ran......ndast om }\frac{\sin \theta_1}{v_1}=\frac{\sin \theta_2}{v_2}.$$


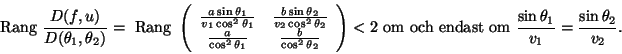
Detta är den enda lokala extrempunkten och måste vara ett globalt minimum för $f$. (Vi har till exempel att $f$ växer då $\theta_1$ går mot noll.) Därför har vi att den snabbaste vägen fås då

$$\frac{\sin \theta_1}{\sin \theta_2} = \frac{v_1}{v_2}.$$
 
 

2001-01-22