En integralekvation

Eftersom vi kan formulera lösningen till matrisproblemet som ${\bf u}={\bf A}^{-1}{\bf f}$ kan man undra om det går att lösa det kontinuerliga problemet analogt, dvs. är det meningsfullt att skriva $u={\cal A}^{-1}f$? Det visar sig att detta är möjligt och att inversen blir en så kallad integraloperator, vilket väl inte är så konstigt. Om man beräknar ``inversen'' till en derivata borde man få en integral. Man kan visa att lösningen till vårt problem kan skrivas:

$$u(t)=\int_0^1G(t,s)f(s)ds,\ \ {\rm med}\ \ G(t,s)=\left\{ \... ... t(1-s),&0\le t\le s\\ s(1-t),&s\le t\le 1 \end{array}\right.$$

$G$ är en så kallad Greenfunktion. Integraloperatorn avbildar alltså funktionen $f$ på $\int_0^1G(t,s)f(s)ds$. Om vi tittar på det enkla fallet då $f(t)=-1$ får vi (vi får dela upp integralen för att ta hand om de två fallen $0\le t\le s$ resp. $s\le t\le 1$):

$$u(t)=-\int_0^1G(t,s)ds= -\int_0^tG(t,s)ds-\int_t^1G(t,s)ds= -\int_0^ts(1-t)ds-\int_t^1t(1-s)ds=\cdots= \frac{t(t-1)}{2}$$

vilket löser problemet och satisfierar randvillkoren.

Rimligtvis borde nu ${\bf A}^{-1}{\bf f}$ svara mot att vi numeriskt har approximerat integralen. Att approximera integraler utgör en del av numerisk analys och detta område benämns vanligen ``numerisk kvadratur''. Om vi vill approximera integralen av en funktion $g$ över intervallet $[a, b]$ brukar detta göras med en viktad summa i stil med:

$$\int_a^b g(s)ds\approx\sum_{k=1}^n w_kg(s_k)$$

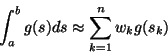
där vikterna $w_k$ och abskissorna $s_k$ väljs på något lämpligt sätt (man vill ha så få $w_k$ och $s_k$ som möjligt givet att felet skall begränsas till en föreskriven nivå till exempel). I matematik-kursen bör Du ha träffat på Riemann-summor vilka kan ses som en typ av kvadraturformel (man approximerar integralen med summan av areorna av en uppsättning rektanglar). Eftersom ${\bf A}^{-1}$ är en full matris svarar en rad i ${\bf A}^{-1}{\bf f}$ (approximationen av $u$ i en punkt) mot en viktad summa av $f(t_1), \ldots , f(t_n)$. Man kan ta reda på vilken kvadraturformel man får, men vi avstår från detta.