Next: Space Discretization
Up: Time Dependent Problems
Previous: Heat Equation
To obtain a numerical method to compute a solution approximation we
start by deriving a variational statement of our problem at
hand.
Multiply (1) by a test function
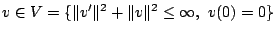 and integrate i.e.
and integrate i.e.
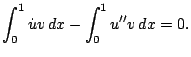 |
(4) |
As usual we assume 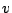 to be smooth enough to allow us to integrate by
parts. We get
to be smooth enough to allow us to integrate by
parts. We get
![$\displaystyle \int_0^1 \dot u v dx - \big[ u'(x)v(x)\big]_0^1 + \int_0^1 u' v' dx = 0.$](img9.gif) |
(5) |
Since 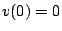 and
and 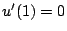 we thus obtain
we thus obtain
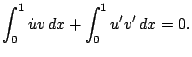 |
(6) |
Hence, the variational formulation of (1) reads: Find
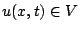 such that for every fixed time
such that for every fixed time 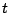
for all 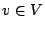 and
and 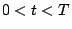 .
.
Mohammad Asadzadeh
2004-08-27
![]() and integrate i.e.
and integrate i.e. 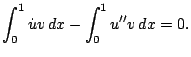
![$\displaystyle \int_0^1 \dot u v dx - \big[ u'(x)v(x)\big]_0^1 + \int_0^1 u' v' dx = 0.$](img9.gif)