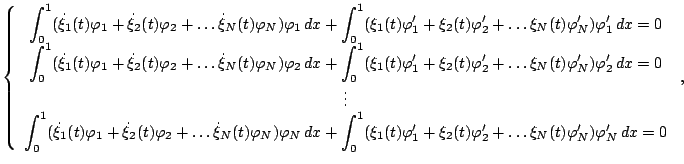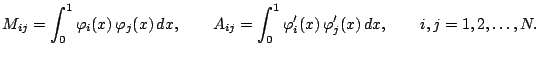Next: Time Discretization
Up: Time Dependent Problems
Previous: Variational Formulation
We next use the variational statement derived previously to make a
discretization of the space dimension. Therefore we introduce a
partition
 ,
,
 of the interval
of the interval
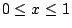 into
into 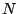 subintervals of equal length
subintervals of equal length 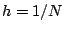 and let
and let
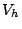 be the corresponding space of continuous piecewise linear
functions vanishing at
be the corresponding space of continuous piecewise linear
functions vanishing at 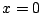 . We now seek a solution approximation
. We now seek a solution approximation
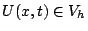 such that for every fixed time
such that for every fixed time 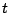
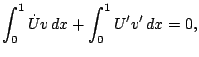 |
(8) |
for all 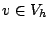 .
.
Further, if
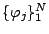 denotes a set of nodal basis functions of
denotes a set of nodal basis functions of
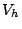 we can expand
we can expand  as
as
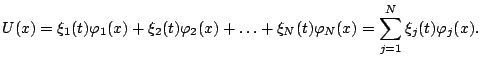 |
(9) |
Notice that the coefficients 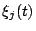 are time dependent but not
space dependent functions.
are time dependent but not
space dependent functions.
Substituting 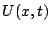 into (7) and choosing test functions
into (7) and choosing test functions
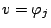 ,
,
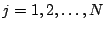 we obtain
we obtain
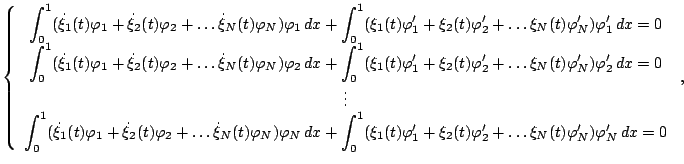 |
(10) |
which is a
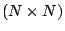 system of ordinary differential equations (ODE)
system of ordinary differential equations (ODE)
where the entries of the matrices
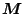 and
and
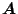 are given by
are given by
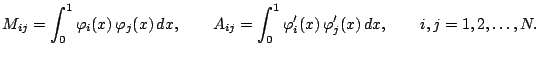 |
(12) |
Here
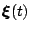 denotes a vector holding the nodal values
denotes a vector holding the nodal values
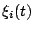 of
of 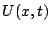 .
.



Next: Time Discretization
Up: Time Dependent Problems
Previous: Variational Formulation
Mohammad Asadzadeh
2004-08-27
![]() ,
,
![]() of the interval
of the interval
![]() into
into ![]() subintervals of equal length
subintervals of equal length ![]() and let
and let
![]() be the corresponding space of continuous piecewise linear
functions vanishing at
be the corresponding space of continuous piecewise linear
functions vanishing at ![]() . We now seek a solution approximation
. We now seek a solution approximation
![]() such that for every fixed time
such that for every fixed time ![]()
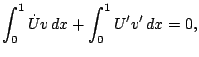
![]() denotes a set of nodal basis functions of
denotes a set of nodal basis functions of
![]() we can expand
we can expand ![]() as
as
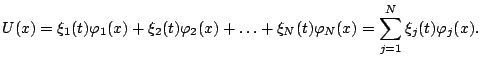
![]() into (7) and choosing test functions
into (7) and choosing test functions
![]() ,
,
![]() we obtain
we obtain