Next: En molekylmodell Up: Var kommer alla positivt Previous: Var kommer alla positivt
![]()
![]()
![]()
Next: En molekylmodell
Up: Var kommer alla positivt
Previous: Var kommer alla
positivt
I nedanstående bild ser vi
![]() kulor/massor med massorna
kulor/massor med massorna
![]() . Kulorna är förbundna med fjädrar som har
fjäderkonstanterna
. Kulorna är förbundna med fjädrar som har
fjäderkonstanterna
![]() .
Systemet svänger longitudinellt (i fjädrarnas längsriktning).
Fjädrarna i ändarna är fast inspända. Vi vill ställa
upp rörelseekvationen för systemet och bortser från gravitation,
friktion etc.
.
Systemet svänger longitudinellt (i fjädrarnas längsriktning).
Fjädrarna i ändarna är fast inspända. Vi vill ställa
upp rörelseekvationen för systemet och bortser från gravitation,
friktion etc.
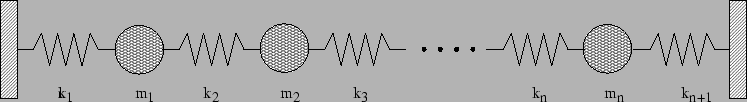
Låt
![]() vara kula nummer
vara kula nummer
![]() :s
avvikelse från jämviktsläget.
:s
avvikelse från jämviktsläget.
![]() beror av tiden
beror av tiden
![]() ,
men för att slippa skriva så mycket sätter vi inte ut
,
men för att slippa skriva så mycket sätter vi inte ut
![]() i
i
![]() .
Om alla
.
Om alla
![]() ligger sålunda kulorna i sina jämviktslägen. Antag nu att
fjädrarna följer Hookes lag så att den återförande
fjäderkraften är proportionell mot fjäderns
längdförändring. Fjäderkonstanten är ju
proportionalitetskonstanten. Fjädrarna på var sida om kula nummer
ligger sålunda kulorna i sina jämviktslägen. Antag nu att
fjädrarna följer Hookes lag så att den återförande
fjäderkraften är proportionell mot fjäderns
längdförändring. Fjäderkonstanten är ju
proportionalitetskonstanten. Fjädrarna på var sida om kula nummer
![]() påverkar densamma med kraften:
påverkar densamma med kraften:
(Ty
![]() är ju längdförändringen av den vänstra fjädern
och en kraft som verkar åt vänster ger minustecken. Analogt ger
en kraft som verkar åt höger plustecken.)
är ju längdförändringen av den vänstra fjädern
och en kraft som verkar åt vänster ger minustecken. Analogt ger
en kraft som verkar åt höger plustecken.)
Använder vi nu Newtons andra lag ser vi att detta skall vara lika med
![]() ,
där vi på vanligt sätt betecknar andraderivatan av
,
där vi på vanligt sätt betecknar andraderivatan av
![]() med avseende på tiden med
med avseende på tiden med
![]() .
Så rörelseekvationerna för kulorna ges, efter lite omskrivning,
av:
.
Så rörelseekvationerna för kulorna ges, efter lite omskrivning,
av:
Låt oss nu skriva ovanstående på matrisform. Vi inför
två matriser, styvhetsmatrisen
![]() och massmatrisen
och massmatrisen
![]() .
.
![\begin{displaymath}
{\bf K}=\left[\begin{array}{cccccc}
k_1+k_2 & -k_2 & 0 & \cd...
...nd{array}\right],\ \ {\bf M}={\rm diag}(m_1, m_2, \ldots, m_n)
\end{displaymath}](img17.gif)
![]() är sålunda en symmetrisk och tridiagonal matris och
är sålunda en symmetrisk och tridiagonal matris och
![]() är diagonal.
är diagonal.
Med dessa matriser och med
![]() ,
kan vi skriva rörelseekvationerna:
,
kan vi skriva rörelseekvationerna:
För att lösa detta begynnelsevärdesproblem måste vi
ha begynnelsepositionerna för massorna, dvs.
![]() och begynnelsefarterna,
och begynnelsefarterna,
![]() .
.
![]() är, som vi sa ovan, en vektor av funktioner som beror av
är, som vi sa ovan, en vektor av funktioner som beror av
![]() .
.
![]() och
och
![]() är med andra ord skalära funktioner av tiden
är med andra ord skalära funktioner av tiden
![]() .
Eftersom
.
Eftersom
![]() och
och
![]() (varför?) får vi från
(varför?) får vi från
![]() :
:
Integrerar vi nu (nollan ger en konstant, kalla den
![]() )
får vi:
)
får vi:
Denna formel säger att summan av den potentiella och den kinetiska energin
är konstant och lika med den totala energin,
![]() (vi förutsätter att systemet är slutet). Detta verkar rimligt;
summan av de kinetiska energierna för varje massa ger den totala kinetiska
energin:
(vi förutsätter att systemet är slutet). Detta verkar rimligt;
summan av de kinetiska energierna för varje massa ger den totala kinetiska
energin:
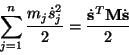
Motsvarande gäller för den potentiella energin; räknar man
på varje fjäder för sig och summerar kommer man (efter lite
räkningar) fram till
![]() .
.
Vi noterar att om minst en kula är i rörelse så är
![]() och den kinetiska energin är positiv, dvs.
och den kinetiska energin är positiv, dvs.
![]() .
Detta innebär ju att
.
Detta innebär ju att
![]() är positivt definit:
är positivt definit:
Vi kan se detta utan att utnyttja fysikaliska resonemang, ty en diagonalmatris
är positivt definit om och endast om den har positiva diagonalelement
(varför?) och massor är ju positiva.
Låt oss nu studera
![]() .
Om
.
Om
![]() ,
dvs. minst en fjäder har förändrad längd så borde
den potentiella energin vara positiv.
,
dvs. minst en fjäder har förändrad längd så borde
den potentiella energin vara positiv.
![]() borde vara positivt definit med andra ord. Att visa att
borde vara positivt definit med andra ord. Att visa att
![]() verkligen är positivt definit är också lätt. Vi utnyttjar
definitionen direkt och får:
verkligen är positivt definit är också lätt. Vi utnyttjar
definitionen direkt och får:
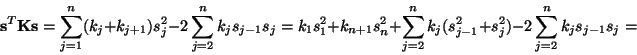
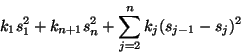
Detta uttryck är positivt om
![]() (varför?).
(varför?).