Matematik
Chalmers
 
Envariabelanalys I, del B, H02

 

Inför tentamen

Tentamensskrivningen kommer att bestå av 5 uppgifter. Skrivningstiden är 4 timmar. Varje uppgift kan ge 6 poäng utom en som kan ge 8 poäng.

Poängsumman från examinationen (tentamen, inlämningsuppgifter samt dugga) avgör betyget på del B av kursen Envariabelanalys I. Betygsgränserna är 25 för trea, 32 för fyra och 40 för femma.

Vid tentamen finns också möjlighet att höja poängen från den löpande examinationen upp till maximalt 18 poäng. Detta sker genom att man löser korrekt valda uppgifter bland sex, som vardera kan ge tre poäng.

Tentamensskrivningen kommer att bestå av tre problem samt två teoriuppgifter.

Teoriuppgifterna kommer att gälla bevis och definitioner som genomgåtts under kursen. Vid tentamen ska man känna till och kunna använda samtliga satser och definitioner.

Följande satser ska dessutom kunna bevisas (H=Häftet):

Sats 1.1 (H sid 1)
Sats 2.2 (H sid 3)
Sats 3.2 (H sid 4)
Sats 3.3 (H sid 4)
Sats 4.1 (H sid 5)
Sats 5.1 (H sid 5)
Sats 5.2 (H sid 5)
Lemma 6.1 (H sid 7)
Sats 8.1 (H sid 9).

Följande begrepp och metoder ur kursen är särskilt viktiga för tillämpningar och vidare studier i matematik (H=Häftet)

Metoder

1. Uppdelning av ett problem i mindre delar för att se att lösningen är en integral. T.ex. för beräkning av volym, båglängd, massa, masscentrum och arbete.
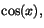
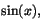
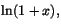
2. Potensserie utvecklingar av e^x, 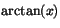$\cos(x),$ $\sin(x),$ $\ln(1+x),$ $\arctan(x)$ och (1+x)^p (sidorna 442, 444, 448, H sidorna 8-9).
3. Taylorutveckling (sid 437). Användning för numerisk approximation (sid 449), beräkning av gränsvärden (Veckoblad 6) och storleksförhållanden (sid 449).
4. Eulers metod (sid 488).
5. Variabelseparation (sid 492, 495).
6. Lösning av y'+a(x)y=b(x) med integrerande faktor. (Veckoblad 3)
7. Lösningsformel för y''+ay+by=0 (sid 541).
8. Teknik och ansättning av partikulärlösning för lösning av y''+ay+by=0=f(t) (Veckoblad 4).
9. Skiss och betydelse av vektorfält till system av differentialekvationer (sidorna 533-535).
10. Användning av vektorer. T.ex ekvation för ett plan, avstånd mellan punkt och plan, punkt och linje samt mellan två linjer (Veckoblad 2). Beräkning av area av en parallellogram och triangel (i rummet).

Definitioner

Båglängd (längd av kurva) (sid 357)
Vektor- och riktningsfält (sidorna 482 och 527)
Talföljd (sid 412, H sid 1)
Konvergens av talföljd (H sid 1)
Serie (sid 412, H sid 2)
Partialsumma till serie (sid 412, H sid 1)
Konvergens och divergens av serie (sid 413, H sid 2)
Summa av konvergent serie (H sid 2)
Positiv serie (H sid 3)
Alternerande serie (sid 420, H sid 3)
Absolutkonvegent serie (H sid 4)
Potensserie kring x=a (sid 423, H sid 5)
Konvergensradie (sid 424, H sid 5)
Taylorpolynom av ordning n kring a (sid 439, H sid 9)
Taylorserie kring a (sid 442)
Fourierpolynom av grad n (sid 459)
Fourierserie (sid 461)
Energi och energispektrum (sid 463)
Stabil och instabil jämviktslösning (sidorna 503 och 528)
Fasplanet (sid 533)
Vektor (sid 606)
Summa av vektorer och mult. med skalär (sidorna 607-608)
Koordinater (eller komponenter) till en vektor (sidorna 609-610)
Längd av vektor (sid 610)
Enhetsvektor (sid 612)
Vektor i n dimensioner (sid 618)
Skalärprodukt (geometriskt och algebraiskt)(sid 620)
Ortogonalitet (sid 622)
Normal till plan (sid 623)
Ortogonal projektion av $\stackrel{\rightarrow}{\mathbf v}$ längs $\stackrel{\rightarrow}{\mathbf u}$ (sid 625)
Kryssprodukt av vektorer i 3 dimensioner (geometriskt och algebraiskt)(sid 630).